Yusuf al-Mu'taman ibn Hud facts for kids
Quick facts for kids Yusuf al-Mu'taman Billah |
|||||
|---|---|---|---|---|---|
| Ruler of Zaragoza | |||||
| Reign | 1081–1085 | ||||
| Predecessor | Ahmad al-Muqtadir | ||||
| Successor | Al-Mustain II | ||||
| Born | Zaragoza | ||||
| Died | 1085 | ||||
|
|||||
| House | Banu Hud | ||||
Abu Amir Yusuf ibn Ahmad ibn Hud (Arabic: أبو عامر يوسف إبن أحمد إبن هود; died around 1085), often called al-Mu'taman, was a king of the Taifa of Zaragoza. He was also a very skilled mathematician. His full royal name, al-Mu'taman Billah, means "Trustee through God."
Al-Mu'taman was the third king from the Banu Hud family. He ruled from 1081 to 1085. This was a time when Muslim Zaragoza was very powerful. He followed in his father's footsteps, inviting many smart people to his court. They lived in the beautiful Aljafería palace, which was known as "the palace of joy."
As king, Al-Mu'taman supported science, philosophy, and art. He was also a great scholar himself. He knew a lot about astrology, philosophy, and especially mathematics. In math, he wrote a very important book called Kitab al-Istikmal, which means "Book of Perfection." This book was one of the most important math works from the al-Andalus region in the 11th century.
Contents
King Al-Mu'taman: His Life and Rule
Becoming King and Dividing the Land
Yusuf was born in Zaragoza, likely in the Aljaferia palace. The exact date of his birth is not known. When his father died in 1081, Yusuf became king. At this time, the Taifa of Zaragoza was at its strongest.
His father split his lands between his two sons. Al-Mu'taman received the western part of the kingdom. This included Zaragoza, Tudela, Huesca, and Calatayud. His brother, al-Mundhir, received the coastal areas. These included Lérida, Monzón, Tortosa, and Dénia.
Dealing with Neighboring Kingdoms
One of the king's first challenges was the King of Aragon, Sancho Ramírez. Sancho wanted to expand his lands south into Zaragoza's territory. To help protect his kingdom, Al-Mu'taman hired a famous soldier named El Cid. El Cid was a mercenary, meaning he fought for money. He had been sent away by King Alfonso VI of Castile.
El Cid started working for Al-Mu'taman's father in 1081. He continued to serve Al-Mu'taman throughout his rule. Al-Mu'taman also asked El Cid to help get back the eastern lands that his brother al-Mundhir had. Al-Mundhir was an ally of Aragon. There were many fights along the border, but neither brother managed to reunite their father's kingdom.
El Cid helped stop the attacks from Aragon until 1083. That year, Sancho managed to capture some important forts. These forts protected Zaragoza, like Graus and Ayerbe. El Cid worked for Yusuf al-Mu'tamin until 1086. Then, he stopped serving the king. The reasons why he left are still debated by historians.
Challenges and the End of His Reign
Al-Mu'taman also tried to make stronger ties with the king of Valencia. He hoped to do this through marriages. However, Valencia was involved in many complicated alliances. King Alfonso VI of Castile used clever diplomacy. He convinced the king of Toledo to give up his city in 1085. In return, Alfonso helped him drive Abu Bakr from Valencia. This meant Toledo was now under Castilian control.
This event cut off the kingdom of Zaragoza from the rest of al-Andalus. This greatly hurt its economy. It also made Zaragoza more open to attacks from Christian kingdoms. The year Valencia was lost was also the year Yusuf al-Mu'tamin died.
Al-Mu'taman's Love for Learning
Kings often had a good education. But Al-Mu'taman and his father were especially good at mathematics. During the Middle Ages in Islam, many ancient Greek texts were translated. These texts covered philosophy, medicine, astronomy, and important math. Both Al-Mu'taman and his father, along with other Islamic translators, added their own ideas to these ancient texts.
For a while, some people thought that Islamic scholars only copied old texts. They believed these scholars did not add new ideas. But later, it was shown that scholars like Ibn Qurra and Al-Mu'taman made their own original contributions. They did more than just pass on old ideas.
His Work in Mathematics
Al-Mu'taman's most important work was his Kitab al-Istikmal (Book of Perfection). This book brought together Greek math ideas from people like Euclid and Archimedes. It also included teachings from Thabit ibn Qurra and Ibn al-Haytham. The book even had some new math rules and proofs that were not found in older writings.
We only have parts of the book today, not the full version. It seems Al-Mu'taman wanted to organize all known ideas in Euclidean geometry into one complete book. He might have listed his sources in a part that is now missing. The parts we have do not mention where he got his information.
The Kitab al-Istikmal was not finished. Still, it was seen as a very important work from the 11th century. One scholar said that if the Istikmal had been finished, other geometry books would not have been needed. Another scholar suggested that mathematicians should read the Istikmal along with famous works like Euclid's Elements.
Because it was not finished, the book was not copied or taught as widely as Euclid's works. A copy was sent to Egypt by Maimonides. From there, it reached Baghdad in the 14th century. However, it did not directly influence later European mathematicians.
The Kitab al-Istikmal discusses many math topics. These include irrational numbers, conic sections, and how to find the area of shapes. It also talks about the volumes of different geometric objects. The book tries to sort mathematics into different groups. It has chapters for arithmetic, geometry, and stereometry (the study of 3D shapes).
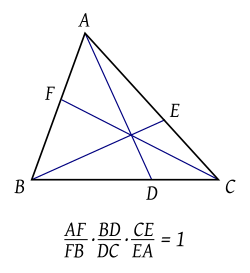
The Kitab al-Istikmal contains the first known mention of Ceva's theorem. This math rule only became known in Europe much later, in 1678. It was published by an Italian geometer named Giovanni Ceva. We do not know if Al-Mu'taman discovered this theorem himself. We also do not know if Ceva found the theorem again on his own.
The theorem says: "Imagine a triangle ABC. Pick points D, E, F on its sides BC, CA, and AB. Draw lines from each corner to the opposite point (AD, BE, CF). These three lines will all meet at one point if and only if a certain math equation is true."
See also
 In Spanish: Al-Mutamán para niños
In Spanish: Al-Mutamán para niños
- List of Arab scientists and scholars