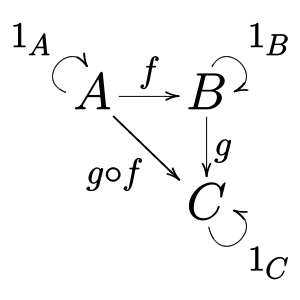Category (mathematics) facts for kids
In mathematics, a category is like a special collection of "things" (called objects) that are connected by "links" (called arrows or morphisms). Think of it as a network where each dot is an object and each line is an arrow.
A category has two main rules:
- You can combine arrows: If you have an arrow from A to B, and another from B to C, you can combine them to get a new arrow from A to C. This is called composition.
- Every object has an "identity" arrow: This is like a special arrow that goes from an object back to itself, and it doesn't change anything when combined with other arrows.
A simple example is the category of sets. Here, the objects are just sets (like a collection of numbers or items), and the arrows are functions that map elements from one set to another.
Category theory is a part of mathematics that studies these categories. It tries to describe all of mathematics using objects and arrows, no matter what they actually represent. This helps mathematicians find hidden connections and similarities between different areas of math that might seem unrelated at first. It's a powerful way to understand how mathematical ideas fit together.
Category theory is also used in computer science, for example, to understand how programming languages work.
Two categories are considered the same if they have the exact same objects, arrows, and ways of combining those arrows. Sometimes, even if they look a little different, two categories can be considered "equivalent" if they behave the same way in category theory.
Well-known categories often have short, bold names. For example:
- Set: This is the category of all sets and functions between them.
- Ring: This is the category of rings (a type of algebraic structure) and special functions called ring homomorphisms.
- Top: This is the category of topological spaces (spaces with a sense of "closeness") and continuous maps (functions that don't break "closeness").
In these examples, the identity arrows are like "do nothing" functions, and combining arrows means combining functions.
A famous book about category theory is Categories for the Working Mathematician by Saunders Mac Lane.
Contents
What is a Category?
A category is made up of a few key parts:
- Objects: These are the "things" in the category. They can be anything, like numbers, sets, groups, or even other categories!
- Morphisms (or arrows): These are the "links" or "connections" between the objects. An arrow goes from a starting object (its domain) to an ending object (its codomain). We write f : a → b to show an arrow f from object a to object b.
- Composition of morphisms: If you have an arrow f from a to b, and another arrow g from b to c, you can combine them to get a new arrow, g ∘ f, which goes directly from a to c. This is like taking two steps to get from a to c.
These parts must follow two important rules, called axioms:
- Associativity: If you have three arrows, f : a → b, g : b → c, and h : c → d, it doesn't matter how you group them when composing. Combining f and g first, then combining the result with h, gives the same result as combining g and h first, then combining f with that result. So, h ∘ (g ∘ f) = (h ∘ g) ∘ f.
- Identity: For every object x, there's a special arrow called the identity morphism (written as 1x) that goes from x to x. When you combine any arrow f with 1x, it doesn't change f. So, 1x ∘ f = f and g ∘ 1x = g.
These rules ensure that categories behave in a consistent and useful way.
Categories: Small and Large
Categories can be described as "small" or "large."
- A category is small if its collection of objects and its collection of arrows can both be thought of as a set. This means you can list them all.
- A category is large if its objects or arrows are too numerous to form a set. For example, the category of all sets is large because there are too many sets to put them all into one set.
- A category is locally small if the collection of arrows between any two specific objects forms a set. Many important categories in mathematics are large but locally small.
Examples of Categories
Here are some examples to help you understand categories better:
- The Category of Sets (Set): This is the most basic category.
* Objects: All possible sets (like {1, 2, 3} or {red, blue}). * Morphisms: All functions between these sets. * Composition: Normal function composition.
- Discrete Categories: Imagine a category where the only arrows are the identity arrows (each object just has an arrow pointing to itself). These are called discrete categories. They are the simplest kind of category.
- Preordered Sets: A preordered set (like numbers with "less than or equal to" ≤) can be a category.
* Objects: The elements of the set (e.g., numbers 1, 2, 3). * Morphisms: An arrow exists from x to y if x ≤ y. * Composition: If x ≤ y and y ≤ z, then x ≤ z, which means you can compose the arrows.
- Monoids: A monoid is an algebraic structure with one operation (like addition or multiplication) and an identity element (like 0 for addition or 1 for multiplication).
* A monoid can be seen as a category with only one object. * Morphisms: The elements of the monoid itself. * Composition: The monoid's operation.
- Groups: A group is like a monoid but every element also has an inverse.
* A group can also be seen as a category with only one object, where every arrow has an inverse. An arrow with an inverse is called an isomorphism.
- Directed Graphs: Any directed graph (like a map with one-way streets) can create a category.
* Objects: The vertices (dots) in the graph. * Morphisms: The paths you can take along the arrows in the graph. * Composition: Connecting paths together.
- Category of Groups (Grp):
* Objects: All possible groups. * Morphisms: Special functions called group homomorphisms that preserve the group structure.
Here's a table of other common categories:
| Category | What are its Objects? | What are its Morphisms (Arrows)? |
|---|---|---|
| Mag | Magmas (basic algebraic structures) | Magma homomorphisms |
| Met | metric spaces (spaces where you can measure distance) | short maps (functions that don't increase distances) |
| Mon | monoids | Monoid homomorphisms |
| Ring | Rings | ring homomorphisms |
| Set | Sets | Functions |
| Top | topological spaces | Continuous functions |
| VectK | vector spaces over a field K | K-linear maps (functions that preserve vector space structure) |
Building New Categories
You can create new categories from existing ones:
Opposite Category
For any category C, you can make a new one called the opposite category (or dual category), written as Cop. It has the exact same objects as C, but all the arrows go in the opposite direction! If f : a → b is an arrow in C, then fop : b → a is an arrow in Cop.
Product Categories
If you have two categories, C and D, you can combine them to form a product category C × D.
- Objects: Are pairs of objects, one from C and one from D.
- Morphisms: Are pairs of arrows, one from C and one from D.
You combine these pairs by combining their parts separately.
Types of Morphisms (Arrows)
Arrows in a category can have special properties:
- A monomorphism (or monic) is like an "injective" function. If f : a → b is a monomorphism, and f combined with two different arrows gives the same result, then those two arrows must have been the same to begin with.
- An epimorphism (or epic) is like a "surjective" function. If f : a → b is an epimorphism, and two different arrows combined with f give the same result, then those two arrows must have been the same.
- An isomorphism is an arrow that has an inverse. This means you can go from a to b with f, and then go back from b to a with another arrow g, and it's like you never moved. If an arrow is an isomorphism, it's both a monomorphism and an epimorphism.
When you see diagrams with objects as points and arrows as lines, these are called commutative diagrams. They help show how arrows relate to each other.
See also
 In Spanish: Categoría (matemáticas) para niños Enriched category Higher category theory Quantaloid Table of mathematical symbols
In Spanish: Categoría (matemáticas) para niños Enriched category Higher category theory Quantaloid Table of mathematical symbols