Glossary of mathematical symbols facts for kids

Kids Encyclopedia Facts

A mathematical symbol is a special sign or picture used in math. These symbols help us show different things like numbers, actions (like adding or subtracting), or how numbers and objects are related. Think of them as a secret code that mathematicians use to write down their ideas!

The most common symbols are the numbers we use every day (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). We also use letters from the Latin alphabet (like a, b, x, y). Long ago, capital letters were used for points in geometry, and small letters were for things that can change (variables) or stay the same (constants).

As math grew, we needed more symbols! So, letters from the Greek alphabet (like π, Σ) and even some Hebrew letters are now used. In math formulas, Latin and small Greek letters are usually italic (slanted), while capital Greek letters are upright. Sometimes, letters are made bold or use special styles like blackboard bold (like ℝ for real numbers) to show different types of math objects.

Some symbols look like letters but have their own special meaning, like Σ (which looks like a Greek S) for "sum." Other symbols come from punctuation marks, like the dot for multiplication. Some, like + and =, were made just for math!

Basic Math Symbols

These are the symbols you'll see most often in math. They're like the building blocks!

Adding and Subtracting

$+$ (plus sign)
- Means addition (adding). Read as "plus." For example, $3 + 2$ is 5.
- Can show a number is positive. For example, $+2$ means positive 2.
$-$ (minus sign)
- Means subtraction (taking away). Read as "minus." For example, $3 - 2$ is 1.
- Can mean the "opposite of" a number. For example, $-2$ is negative 2.

Multiplying and Dividing

$\times$ (multiplication sign)
- In basic math, means multiplication. Read as "times." For example, $3 \times 2$ is 6.
- In geometry and linear algebra, it means the cross product.
$\cdot$ (dot)
- Also means multiplication. Read as "times." For example, $3 \cdot 2$ is 6.
- In geometry and linear algebra, it means the dot product.
$\pm$ (plus–minus sign)
- Means "plus or minus." It shows that a value can be either added or subtracted.
- Can show a range of values. For example, $10 \pm 2$ means a value between 8 and 12.
$\div$ (division sign)
- Means division. It's common in English-speaking countries but less used in higher math.
$:$ (colon)
- Shows a ratio between two amounts. For example, 1:2 means "1 to 2."
- In some countries, it can mean division.
$/$ (slash)
- Means division. Read as "divided by" or "over." For example, $3 / 2$ .
- In probability theory, it shows a conditional probability. For example, 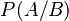$P(A/B)$ means the probability of A happening, given that B has happened.

Roots and Powers

$\sqrt$ (square-root symbol)
- Means "the square root of." For example, $\sqrt2$ is the number that, when multiplied by itself, equals 2.
$\sqrt$ (radical symbol)
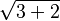- Also means square root. For example, $\sqrt{3+2}$ .
- With a small number above and to the left, it means an "nth root." For example, $\sqrt[7]{3}$ is the 7th root of 3.
$^$ (caret)
- Used for exponentiation (powers) when you can't easily write a small number above. For example, $x^y$ means x to the power of y.

Comparing Things

These symbols help us show how numbers or objects relate to each other in terms of size or value.

Equality and Similarity

$=$ (equals sign)
- Means equality. It shows that two things are the same value.
- Can be used to name a math object. For example, "let Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): x=5 ."
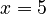$\neq$ (not-equal sign)
- Means inequality. It shows that two things are not equal.
$\approx$
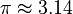- Means "approximately equal to." For example, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \pi \approx 3.14 .
$~$ (tilde)
- Between two numbers, it can mean "approximately equal" or "has the same size."
- Can show that two functions or shapes are similar.
$\equiv$ (triple bar)
- Means an identity, which is an equality that is always true, no matter the values of the variables.
- In modular arithmetic, it means "congruent to."
$\cong$
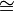
- Can mean "is isomorphic to" (meaning two math structures are basically the same).
- In geometry, it means "is congruent to" (meaning two shapes are the same size and shape).

Greater or Less Than

$<$ (less-than sign)
- Means "less than." For example, $3 < 5$ .
$>$ (greater-than sign)
- Means "greater than." For example, $5 > 3$ .
$\leq$
- Means "less than or equal to." For example, $x \leq 5$ means x can be 5 or any number smaller than 5.
$\geq$
- Means "greater than or equal to." For example, $x \geq 5$ means x can be 5 or any number larger than 5.
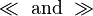
$\ll \text{ and }\gg$
- Mean "much less than" and "much greater than." This usually means one quantity is so much smaller (or larger) than the other that it can be ignored.

Sets and Logic

These symbols are used when we talk about groups of things (sets) or when we use logical reasoning.

Set Theory Symbols

$\emptyset$
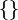- Means the empty set, which is a set with no elements in it. It can also be written as $\{\}$ .
$#$ (number sign)
- Can mean the number of elements in a set. For example, 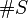$\#S$ is the size of set S.
$\in$
- Means "is in" or "belongs to." For example, 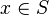$x\in S$ means x is an element of set S.
$\notin$
- Means "is not in." For example, 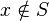$x\notin S$ means x is not an element of set S.
$\subset$
- Can mean that set A is a subset of set B (all elements of A are in B), and A might be equal to B.
- Can also mean that A is a proper subset of B (all elements of A are in B, but A is not equal to B).
$\subseteq$
- Means that set A is a subset of set B, and it can be equal to B.
$\cup$
- Means set-theoretic union. $A\cup B$ is a new set with all the elements from set A and set B combined.
$\cap$
- Means set-theoretic intersection. 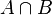$A\cap B$ is a new set with only the elements that are in both set A and set B.
$∖$ (backslash)
- Means Set difference. 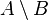$A\setminus B$ is the set of elements that are in A but not in B.
$\times$ (multiplication sign)
- Means the Cartesian product of two sets. 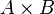$A\times B$ is a set of all possible pairs where the first item is from A and the second is from B.

Basic Logic Symbols

$\neg$ (not sign)
- Means logical negation, read as "not." If a statement E is true, 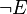$\neg E$ is false.
$\lor$ (descending wedge)
- Means logical or, read as "or." 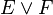$E\lor F$ is true if E is true, or F is true, or both are true.
$\land$ (wedge)
- Means logical and, read as "and." 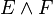$E\land F$ is true only if both E and F are true.
$\forall$ (turned A)
- Means universal quantification, read as "for all" or "for every." 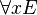$\forall x E$ means E is true for every possible value of x.
$\exists$
- Means existential quantification, read as "there exists." 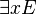$\exists x E$ means there is at least one value of x for which E is true.
$\exists!$
- Means "there exists exactly one." 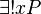$\exists ! x P$ means there is only one x for which P is true.
$\Rightarrow$
- Means material conditional, read as "implies." $P \Rightarrow Q$ means if P is true, then Q must also be true.
$\Leftrightarrow$
- Means logical equivalence, read as "is equivalent to" or "if and only if." $P \Leftrightarrow Q$ means P and Q are either both true or both false.

Special Number Sets

These symbols use a special "blackboard bold" style to represent important sets of numbers.

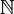
$\mathbb N$
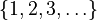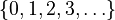- Means the set of natural numbers. This can be Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \{1, 2, 3, \ldots \} or sometimes Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \{0, 1, 2, 3, \ldots \} .
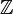
$\mathbb Z$
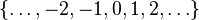- Means the set of integers. These are whole numbers, including negative numbers and zero: Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \{\ldots, -2, -1, 0, 1, 2, \ldots \} .
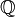
$\mathbb Q$
- Means the set of rational numbers. These are numbers that can be written as a fraction of two integers (like 1/2 or 3/4).
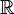
$\mathbb R$
- Means the set of real numbers. This includes all rational and irrational numbers (like π or √2).
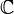
$\mathbb C$
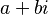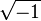- Means the set of complex numbers. These are numbers that can be written as $a + bi$ , where 'a' and 'b' are real numbers and 'i' is the imaginary unit ( $\sqrt{-1}$ ).

Calculus Symbols

Calculus is a branch of math that deals with change. These symbols are used to describe how things change.

$□'$
- This is Lagrange's notation for the derivative. If 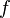$f$ is a function, 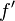$f'$ (read as "f prime") is its derivative, showing how fast the function's value changes.
$\dot \Box$
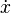- This is Newton's notation, often used for a derivative with respect to time. If $x$ changes over time, $\dot x$ is its speed.
$d □ / d □$
- This is Leibniz's notation for the derivative. 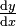$\textstyle \frac{\mathrm{d}y}{\mathrm{d}x}$ means the derivative of y with respect to x. It shows how y changes as x changes.
$\partial □ / \partial □$
- This is for a Partial derivative. If a function has many variables, this symbol shows the derivative with respect to just one variable, treating the others as constants.
$\overline\Box$
- Can mean the Complex conjugate of a complex number. For example, $\overline{a+bi} = a-bi$ .
- Can mean the Mean value (average) of a set of numbers.
$\to$
- Can show a function goes from one set to another. For example, 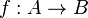$f:A \to B$ means function f maps from set A to set B.
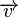- Can mean a vector. For example, $\overrightarrow v$ .
$\mapsto$
- Used to define a function without giving it a name. For example, $x\mapsto x^2$ means the function that takes x and gives back x squared.
$○$
- Means Function composition. If f and g are functions, $g\circ f$ means applying f first, then applying g to the result.
$\int$
- Means an integral. This is used to find the "total" or "area under a curve."
$\boldsymbol{\nabla}$
- Called nabla or del, it's an operator used in multivariable calculus to find the gradient (how steeply a function changes).

Sums and Products

These symbols are used for adding or multiplying many terms together.

$\sum$ (Sigma notation)
- Means sum. It's used to add up a list of numbers. For example, 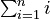Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \textstyle \sum_{i=1}^n i means add up all numbers from 1 to n.
$\prod$ (Capital-pi notation)
- Means product. It's used to multiply a list of numbers. For example, 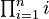Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \textstyle \prod_{i=1}^n i means multiply all numbers from 1 to n.

Brackets and Parentheses

Brackets and parentheses are super important in math to group things and show what goes together. Their meaning often depends on their shape and what's inside them.

Parentheses ( )

$(□)$
- Used to group parts of an expression to show the order of operations. For example, 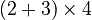Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (2+3)\times 4 means add 2 and 3 first, then multiply by 4.
$□(□)$
- Used for Functional notation. If 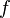$f$ is a function, 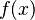$f(x)$ means the value of the function f at x.
$(□, □)$
- Can mean an ordered pair of math objects, like coordinates on a graph (x, y).
- If 'a' and 'b' are numbers, 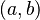$(a,b)$ can mean an open interval (all numbers between a and b, but not including a or b).
$\binom{\Box}{\Box}$
- Means a binomial coefficient. $\binom{n}{k}$ is read as "n choose k" and tells you how many ways you can choose k items from a set of n items.

Square Brackets [ ]

$[□]$
- Can be used like parentheses to group things.
- Can mean an equivalence class.
- If 'x' is a real number, $[x]$ can mean the integral part of x (the whole number part).
$[□, □]$
- If 'a' and 'b' are numbers, $[a,b]$ means a closed interval (all numbers between a and b, including a and b).
- In group theory or ring theory, it can mean a commutator.

Braces { }

${□, ..., □}$
- Used in Set-builder notation to list the elements of a set. For example, 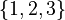Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \{1, 2, 3\} is the set containing 1, 2, and 3.
${□ : □}$ or ${□ | □}$
- Used in Set-builder notation to define a set based on a rule. For example, 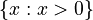Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \{x : x > 0\} means "the set of all x such that x is greater than 0."
Single brace
- Used to group simultaneous equations or to define a Piecewise function (a function defined by different rules for different parts of its domain).

Other Brackets

$|□|$
- Means Absolute value. 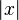$|x|$ is the distance of x from zero, always positive. For example, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): |-5| = 5 .
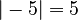- Can also mean the number of elements in a set (its cardinality).
$||□||$
- Means the norm of an element, which is like its "length" or "size" in a more complex math space.
$⌊□⌋$
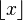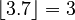- Means the Floor function. $\lfloor x\rfloor$ is the greatest integer that is less than or equal to x. For example, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \lfloor 3.7\rfloor = 3 .
$⌈□⌉$
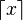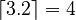- Means the Ceiling function. $\lceil x\rceil$ is the smallest integer that is greater than or equal to x. For example, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \lceil 3.2\rceil = 4 .
$⟨□⟩$
- Can mean a generated object. For example, 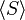$\langle S \rangle$ is the smallest structure (like a group or vector space) that contains all elements of S.
$⟨□, □⟩$
- Means the inner product of two elements, which is a way to multiply vectors and get a scalar.

Symbols Not in Formulas

Some symbols are used more like punctuation in math writing, or as shortcuts for common phrases.

$■ , □$
- Used to mark the end of a math proof. It's like saying "we're done proving this!"
$∴$
- Means "therefore." It shows that one statement leads to another.
$∵$
- Means "because" or "since." It shows that one statement is true because of another.
$\propto$
- Means "is proportional to." If A is proportional to B, it means A changes directly with B.

Other Useful Symbols

$!$
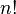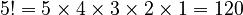- Means Factorial. If 'n' is a positive whole number, $n!$ is the product of all positive integers up to n. For example, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 .
$|$
- Means Divisibility. 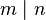$m\mid n$ means that m divides n exactly (with no remainder).
- In set-builder notation, it means "such that."
$∥$
- Means parallelism in geometry. If two lines are parallel, they never meet.
$\perp$
- Means perpendicularity and orthogonality. If two lines or objects are perpendicular, they meet at a right angle (90 degrees).