Hypercomplex number facts for kids
In mathematics, a hypercomplex number is a special kind of number that extends the idea of real numbers and complex numbers. Think of them as numbers that live in a space with more than two dimensions. They are part of a mathematical system called an "algebra" over real numbers. Studying these numbers in the late 1800s helped create the modern theory of group representation, which is important in many areas of math and science.
Contents
History of Hypercomplex Numbers
In the 1800s, mathematicians started discovering new types of numbers beyond the familiar real and complex numbers. These included quaternions, tessarines, coquaternions, biquaternions, and octonions. The term "hypercomplex number" was created to describe all these new number systems.
The effort to understand and classify these numbers began in 1872 with Benjamin Peirce and his son Charles Sanders Peirce. They found that certain special numbers, called nilpotents (numbers that become zero when multiplied by themselves enough times) and idempotents (numbers that stay the same when multiplied by themselves), were very useful for sorting hypercomplex numbers.
A method called the Cayley–Dickson construction showed how to build complex numbers, quaternions, and octonions step-by-step from the real numbers. However, mathematicians like Hurwitz and Frobenius discovered that there are limits to how many dimensions these special number systems can have while still behaving nicely. Their theorems showed that the most "well-behaved" systems can only exist in 1, 2, 4, or 8 dimensions.
Later, matrix algebra became a powerful tool for understanding hypercomplex numbers. For example, 2x2 matrices (grids of numbers) were found to act just like coquaternions. In 1907, Joseph Wedderburn proved that many hypercomplex systems could be represented using matrices. Because of this, the term "associative algebra" became more common than "hypercomplex system" for these types of numbers. However, some hypercomplex numbers, like octonions, are "non-associative," meaning the order of multiplication matters more.
Historians like Thomas W. Hawkins Jr., Emmy Noether, and Karen Parshall have shown how important hypercomplex numbers were in leading to modern ideas like Lie groups and group representation theory.
What is a Hypercomplex Number?
Simply put, a hypercomplex number is a number that belongs to a special kind of mathematical system called an "algebra." This algebra is built using real numbers and has a limited number of dimensions.
Imagine a number like a + bi, where a and b are real numbers, and i is the imaginary unit (where i² = -1). This is a complex number, and it lives in two dimensions. Hypercomplex numbers extend this idea to more dimensions, using a basis of numbers like {1, i₁, i₂, ...}.
Two-Dimensional Hypercomplex Numbers
There are exactly three main types of two-dimensional hypercomplex numbers that are built from real numbers:
- The ordinary complex numbers: These are numbers like a + bi, where i² = -1. They are used a lot in physics and engineering.
- The split-complex numbers: These are numbers like a + bj, where j² = +1. Unlike complex numbers, they have special properties like "zero divisors" (two non-zero numbers that multiply to zero). They are useful in areas like special relativity.
- The dual numbers: These are numbers like a + bε, where ε² = 0. These numbers are used in some areas of geometry and calculus.
Out of these three, only the complex numbers can be used for division in the same way real numbers can. The other two have special numbers that can't be divided by.
Higher-Dimensional Examples
Clifford Algebras
Clifford algebras are a powerful way to create many hypercomplex number systems. They are built from a basic set of elements, like e₁, e₂, etc., where each element can square to +1, -1, or 0. When you combine these elements through multiplication, you get a larger system.
These algebras are very useful in physics, especially for understanding things like rotations, phases, and spin in classical and quantum mechanics, and in electromagnetic theory and relativity.
Some examples of Clifford algebras you might recognize are:
- The complex numbers
- The split-complex numbers
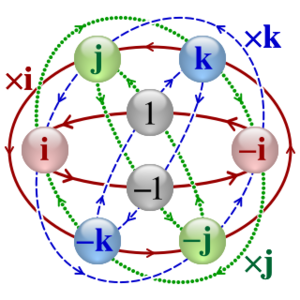
- The quaternions
- The spacetime algebra (used in relativity)
One cool thing about Clifford algebras is that they keep a property called "associativity" (where (a × b) × c = a × (b × c)) no matter how many dimensions they have. This is different from some other ways of building hypercomplex numbers.
Cayley–Dickson Construction
The Cayley–Dickson construction is another way to build new number systems, doubling the dimensions each time. It starts with real numbers, then builds complex numbers, then quaternions (4 dimensions), then octonions (8 dimensions), and then sedenions (16 dimensions).
However, as you go to higher dimensions with this method, some familiar rules of arithmetic start to break down:
- Quaternion multiplication is not commutative (meaning a × b is not always the same as b × a).
- Octonion multiplication is not associative (meaning (a × b) × c is not always the same as a × (b × c)).
- Sedenions even have "zero divisors" (non-zero numbers that multiply to zero), which means you can't divide by them.
This construction can also create "split algebras" like split-complex numbers, split-quaternions, and split-octonions, which have different properties, often including zero divisors.
Tensor Products
You can also create new hypercomplex number systems by combining existing ones using something called a tensor product. It's like multiplying two number systems together to get a bigger one.
For example, if you combine complex numbers with themselves, you get four-dimensional bicomplex numbers. Combining complex numbers with quaternions gives you eight-dimensional biquaternions.
Other Examples
- Bicomplex numbers: These are 4-dimensional numbers that can also be seen as 2-dimensional over the complex numbers.
- Multicomplex numbers: These are a family of numbers that extend the idea of complex numbers to many dimensions.
- Composition algebras: These are algebras that have a special property related to their "size" or "norm."
See also
- Sedenions
- Thomas Kirkman
- Georg Scheffers
- Richard Brauer
- Hypercomplex analysis