Kepler's laws of planetary motion facts for kids

Kids Encyclopedia Facts

In astronomy, Kepler's laws of planetary motion are three important rules that describe how planets move around the Sun. These laws were discovered by Johannes Kepler in the early 1600s. They changed how people understood the Solar System.

Before Kepler, many scientists, like Nicolaus Copernicus, thought planets moved in perfect circles. They also used complex ideas like "epicycles" to explain why planets sometimes seemed to move backward. Kepler's laws showed that planets actually move in elliptical orbits, which are like stretched circles. His laws also explained how the speed of planets changes as they orbit.

The three laws are:

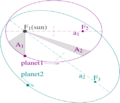
The orbit of a planet is an ellipse (a stretched circle). The Sun is at one of the two special points inside the ellipse, called foci.
A line connecting a planet and the Sun sweeps out equal areas in equal amounts of time. This means a planet moves faster when it's closer to the Sun and slower when it's farther away.
The square of a planet's orbital period (the time it takes to go around the Sun once) is related to the cube of the average distance of its orbit from the Sun. This means planets farther from the Sun take much longer to complete one orbit.

Kepler figured out these laws by carefully studying the orbit of Mars. He then realized that all other planets in our Solar System also follow these same rules. Later, in 1687, Isaac Newton showed that Kepler's laws were a natural result of his own law of universal gravitation and laws of motion.

Kepler and Copernicus: What Changed?
How the Laws Got Their Names
History of Discovery
Kepler's First Law: Elliptical Orbits
Kepler's Second Law: Equal Areas in Equal Times
Kepler's Third Law: Period and Distance
Newton and Planetary Motion
Images for kids
See also

Kepler and Copernicus: What Changed?

Johannes Kepler made big improvements to the ideas of Nicolaus Copernicus. Copernicus correctly said that planets orbit the Sun. However, he believed:

Planets moved in perfect circles, sometimes with smaller circles called epicycles.
The Sun was roughly at the center of these orbits.
The speed of a planet in its main orbit was always the same.

Kepler used careful observations and math to show that these ideas were not quite right. He found that:

Planetary orbits are not circles with epicycles. They are ellipses.
The Sun is not at the center of the orbit. It is at a special point called a focal point within the elliptical orbit.
A planet's speed is not constant. It changes. However, the area speed (how fast the line from the Sun to the planet sweeps out area) is constant.

For example, Earth's orbit is slightly elliptical. This is why the time from the March equinox to the September equinox (about 186 days) is a bit longer than the time from the September equinox to the March equinox (about 179 days).

How the Laws Got Their Names

It took almost 200 years for Kepler's discoveries to be called "laws." The French writer Voltaire was one of the first to use the term "laws" for these ideas in 1738.

The set of three laws we know today was fully put together by Robert Small in 1814. He added the third law to the group.

Interestingly, what we call "Kepler's Second Law" today was not the only version Kepler had. He had a "distance law" and an "area law." The "area law" is the one that became the Second Law in the set of three.

History of Discovery

Kepler published his first two laws in 1609. He found them by studying the very detailed observations of the sky made by Tycho Brahe. Kepler's third law was published later, in 1619.

Kepler originally believed in the Copernican model, which said orbits were circular. But Brahe's observations of Mars were so precise that Kepler couldn't make them fit a circular orbit. Mars has a more stretched-out orbit (higher eccentricity) than most other planets, which made it a good planet to study for this discovery. This led to his first law.

In 1621, Kepler noticed that his third law also applied to the four brightest moons of Jupiter, which were discovered by Galileo. Other scientists, like Godefroy Wendelin, also observed this.

Isaac Newton later realized that Kepler's second law (the area law) was true for any force that pulls an object directly towards a central point. The other two laws, however, specifically depend on the force of gravity getting weaker with the square of the distance.

Kepler's First Law: Elliptical Orbits

Kepler's first law says:

The orbit of every planet is an ellipse with the Sun at one of the two foci.

Kepler's first law shows the Sun at one of the special points (foci) of an elliptical orbit.

An ellipse looks like a flattened circle. It has two special points inside called "foci" (plural of focus). The Sun is always at one of these two focal points, not in the exact center of the ellipse.

When a planet is closest to the Sun in its orbit, this point is called perihelion. When it is farthest away, it is called aphelion.

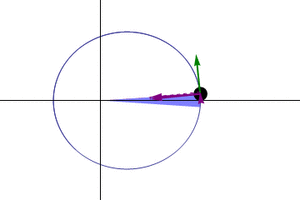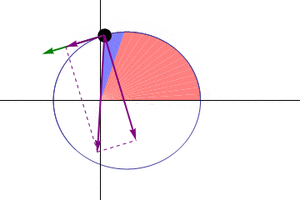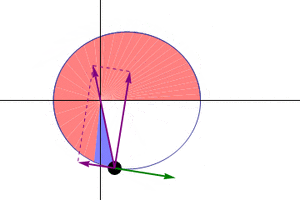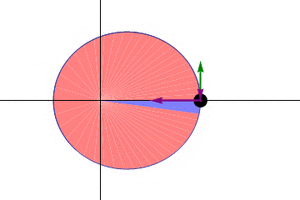
Kepler's Second Law: Equal Areas in Equal Times

Kepler's second law states:

A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.

The same (blue) area is swept out in a fixed time period. The green arrow is velocity. The purple arrow directed towards the Sun is the acceleration. The other two purple arrows are acceleration components parallel and perpendicular to the velocity.

This law means that a planet does not move at a constant speed throughout its orbit. When a planet is closer to the Sun, it moves faster. When it is farther away, it moves slower.

Imagine drawing a line from the Sun to a planet. As the planet moves, this line sweeps out an area. Kepler's second law says that if you pick two equal periods of time (for example, 30 days), the area swept out by this line will be the same, no matter where the planet is in its orbit. This is why the planet has to speed up when it's closer to the Sun.

This law is true because of something called the conservation of angular momentum. This is a basic rule in physics that applies when a force pulls an object directly towards a central point, like gravity pulling a planet towards the Sun.

Orbits of planets with varying eccentricities.
Low	High
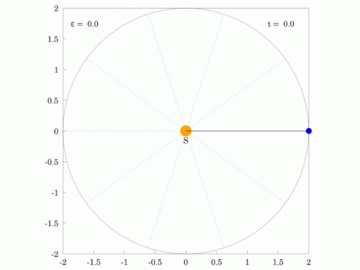
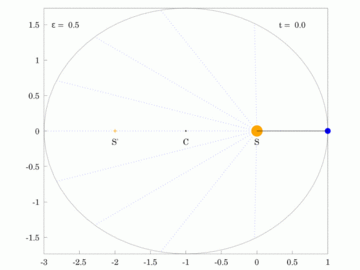
Planet orbiting the Sun in a circular orbit (e=0.0)	Planet orbiting the Sun in an orbit with e=0.5
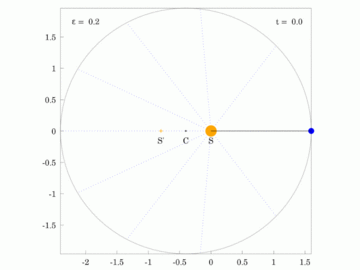
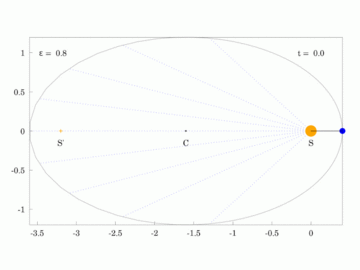
Planet orbiting the Sun in an orbit with e=0.2	Planet orbiting the Sun in an orbit with e=0.8
The red ray rotates at a constant angular velocity and with the same orbital time period as the planet, 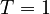$T=1$ . S: Sun at the primary focus, C: Centre of ellipse, S': The secondary focus. In each case, the area of all sectors depicted is identical.

Kepler's Third Law: Period and Distance

Kepler's third law states:

The ratio of the square of an object's orbital period with the cube of the semi-major axis of its orbit is the same for all objects orbiting the same primary.

This law connects how long a planet takes to orbit the Sun (its period) with its average distance from the Sun. The "semi-major axis" is half of the longest diameter of the elliptical orbit. It's like the average distance of the planet from the Sun.

Kepler called this the harmonic law because he was trying to find the "music of the spheres." He believed that the universe followed precise mathematical and musical rules.

Using Isaac Newton's law of gravity, we can show why this law works. For a planet orbiting the Sun, the force of gravity pulling it towards the Sun is balanced by the force that keeps it moving in a circle (centripetal force). This balance leads to Kepler's third law.

The law can be written as a formula: 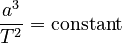Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{a^3}{T^2} = \text{constant} Here, a is the semi-major axis (average distance) and T is the orbital period. This "constant" value is the same for all planets orbiting the Sun.

The following table shows the data Kepler used to figure out his law:

Data used by Kepler (1618)
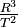Planet	Mean distance to sun (AU)	Period (days)	${\textstyle \frac{R^3}{T^2}}$ (10^-6 AU³/day²)
Mercury	0.389	87.77	7.64
Venus	0.724	224.70	7.52
Earth	1	365.25	7.50
Mars	1.524	686.95	7.50
Jupiter	5.20	4332.62	7.49
Saturn	9.510	10759.2	7.43

Kepler was amazed when he found this pattern. He wrote: "I first believed I was dreaming... But it is absolutely certain and exact that the ratio which exists between the period times of any two planets is precisely the ratio of the 3/2th power of the mean distance."

Here are more modern estimates for the same values:

Modern data
Planet	Semi-major axis (AU)	Period (days)	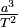${\textstyle \frac{a^3}{T^2}}$ (10^-6 AU³/day²)
Mercury	0.38710	87.9693	7.496
Venus	0.72333	224.7008	7.496
Earth	1	365.2564	7.496
Mars	1.52366	686.9796	7.495
Jupiter	5.20336	4332.8201	7.504
Saturn	9.53707	10775.599	7.498
Uranus	19.1913	30687.153	7.506
Neptune	30.0690	60190.03	7.504

Newton and Planetary Motion

Isaac Newton later showed that Kepler's laws were a direct result of his own law of universal gravitation. Newton's law states that every object in the universe attracts every other object. The strength of this attraction depends on their masses and the distance between them.

Newton's law explained that:

Every planet is pulled towards the Sun by gravity.
The strength of this pull depends on the planet's mass and gets weaker the farther away it is from the Sun (it follows an "inverse square law").

Because planets have much smaller masses than the Sun, their orbits follow Kepler's laws very closely. Newton's work improved on Kepler's model. It helped scientists understand why planets move the way they do, not just how they move.

Images for kids

Illustration of Kepler's laws with two planetary orbits.