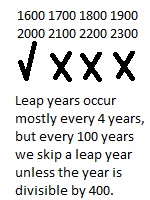Leap year facts for kids
A leap year is a year with an extra day added to it. Most of the world uses the Gregorian calendar. In a normal year, there are 365 days. But a leap year has 366 days.
The extra day is February 29. It is added to the month of February. Normally, February has 28 days. In a leap year, it has 29 days. The extra 29th day is called a leap day. It falls on the same day of the week as February 1. Also, in a leap year, the months of January, April, and July all start on the same day of the week.
A leap year happens about once every four years. So, a leap year can usually be evenly divided by four. For example, 2012 was a leap year. However, there are special rules for years that end in "00". A year is not a leap year if it can be divided by 100 but not by 400. This is why 1600, 2000, and 2400 are leap years. But 1700, 1800, and 1900 were not leap years.
We have leap years because the Earth takes a little longer than 365 days to go around the Sun. It actually takes about 365 and a quarter days (365.24219 days). Without leap years, the seasons would start about one day earlier on the calendar every four years. After many years, spring would start in the middle of winter!
Some countries use a lunar calendar. This calendar is based on the moon, not the Sun. These calendars also have leap years. They add an extra lunar month instead of a day.
The Julian Calendar
Around 45 BC, Julius Caesar changed the old Roman calendar. He made it a solar calendar, which means it followed the Sun. This removed the need for adding extra months often.
Caesar's rule for leap years was simple. He added a leap day every four years. This calendar was used for about 1600 years. However, it was not perfectly accurate. The Julian year was 365.25 days long. The actual time it takes for Earth to orbit the Sun is slightly less. This caused the calendar to slowly drift. It became off by about three days every 400 years.
In the Julian calendar, the leap day was handled differently. It was not always at the end of February. Sometimes, it was placed within February. Also, the leap day was not always counted as an extra day. This meant a leap year was still seen as having 365 days for some purposes. Over time, these practices changed. Today, February 29 is clearly counted as an extra day.
The Gregorian Calendar
The Gregorian calendar is the main calendar used in most of the world today. In this calendar, most years that can be divided by 4 are leap years. In a leap year, February has 29 days instead of 28. This extra day helps to balance our calendar with the Earth's orbit. The Earth takes almost 6 hours longer than 365 days to go around the Sun.
However, the Earth's orbit is not exactly 365.25 days. It's a tiny bit less. Because of this, the Gregorian calendar has special rules for leap years:
- Every year that can be exactly divided by four is a leap year.
- But, if a year can be exactly divided by 100, it is NOT a leap year.
- Unless that year can also be exactly divided by 400. Then it IS a leap year.
For example, the years 1700, 1800, and 1900 were not leap years. But the years 1600 and 2000 were leap years. The years 2100, 2200, and 2300 will not be leap years. But 2400 will be.
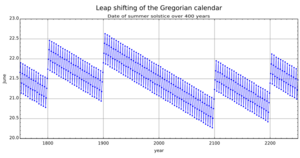
This rule helps to correct the small error from the Julian calendar. It removes three leap days every 400 years. This makes the average year length much closer to the actual time the Earth takes to orbit the Sun.
The Gregorian calendar was created to keep the March equinox (when spring begins) on or near March 21. This is important for calculating the date of Easter. Easter is celebrated on the Sunday after the first full moon that happens on or after March 21.
Related pages
Images for kids
-
The algorithm (steps) to figure out if a year is a leap year in the Gregorian calendar.
-
A Swedish pocket calendar from 2008 showing February 29.
-
February 1900 calendar showing that 1900 was not a leap year.
-
In older church books, feast days after February 24 were celebrated one day later in a leap year.
-
A cartoon from 1903 about leap year traditions.
-
A postcard from 1908 showing a woman "capturing" a man.
-
A postcard from 1908 showing women waiting for January 1.
-
A postcard from 1908 showing women preparing.
See also
In Spanish: Año bisiesto para niños
