Stationary-action principle facts for kids

The stationary-action principle, also called the principle of least action, is a big idea in physics. It helps us understand how things move. Imagine a ball rolling down a hill. This principle says that the path the ball takes is special. It's the path where a value called "action" doesn't change much, even if you try to make tiny changes to the path.

This principle helps scientists figure out the equations of motion. These are the math rules that describe how objects move. It works for many areas of physics, like Newtonian mechanics (how everyday objects move), Lagrangian mechanics, and Hamiltonian mechanics. It even applies to general relativity (how gravity works on a large scale) and quantum field theory (how tiny particles behave).

The idea of stationary action was very important for developing quantum mechanics. In 1933, physicist Paul Dirac showed how it connects to quantum ideas. Later, Julian Schwinger and Richard Feynman used it to understand quantum electrodynamics, which describes how light and matter interact.

This principle is still a key part of modern physics and mathematics. You can find it in thermodynamics (heat and energy), fluid mechanics (how liquids and gases move), and even string theory. Ideas like Maupertuis' principle and Hamilton's principle are examples of the stationary-action principle.

The concept actually started with ideas about light. In ancient Greece, Euclid noticed that when light reflects off a mirror, the angle it hits the mirror is the same as the angle it bounces off. Later, Hero of Alexandria showed that this path was the shortest and took the least time.

Many people give credit to Pierre Louis Maupertuis for explaining the principle of least action in the 1740s. But Leonhard Euler also wrote about it around the same time. Even earlier, Gottfried Leibniz discussed similar ideas almost 40 years before them.

What Is the Action Principle?

As a system moves, it follows a path (red line) through its possible arrangements. The action along this path is "stationary," meaning it doesn't change much if you make tiny adjustments to the path.

The "action" of a physical system is a special value. We use the symbol 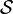for it. You can think of it as a total "cost" or "effort" for a system to go from one state to another over time. It's calculated by adding up another value called the "Lagrangian" over a period of time.

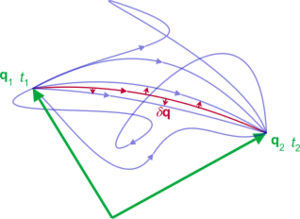
Imagine a system moving from a starting point at time t₁ to an ending point at time t₂. The action is found by doing a special type of sum (an integral) of the Lagrangian L during that time. The Lagrangian depends on where the system is and how fast it's moving.

The principle says that the actual path a system takes is the one where the action 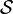is "stationary." This means that if you make a very small change to the path, the action won't change much at all. It's like being at the top or bottom of a hill – a small step won't change your height much.

So, in math, we write it like this: 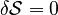Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \delta \mathcal{S} = 0 } The symbol δ (delta) means a "small change." This means the action has no first-order change.

It's important to know that "stationary action" doesn't always mean the least action. Sometimes it can be a maximum, or a saddle point. But for short parts of the path, it often is the minimum.

When we put the definition and the principle together, it looks like this: 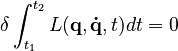Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\displaystyle \delta \int_{t_1}^{t_2} L(\mathbf{q}, \mathbf{\dot{q}},t) dt = 0 } Here, the "path" is simply the way the system moves over time. It's like drawing a line that shows where the system is at every moment.

How the Principle Developed

Many smart people helped develop the action principle over centuries.

Lagrange and Hamilton's Contributions

Joseph-Louis Lagrange was a mathematician who, in 1760, used a new type of math called calculus of variations to solve problems about motion. In 1788, he wrote down general Lagrangian equations of motion for mechanical bodies.

Later, in the 1830s, William Rowan Hamilton used this idea. He applied the principle to a special function called the Lagrangian function (which is kinetic energy minus potential energy). This helped him find the important Euler–Lagrange equations that we still use today.

Understanding Stationary Points

In 1842, Carl Gustav Jacobi wondered if the variational principle always found the smallest action, or if it could find other "stationary points" (like a maximum or a saddle point). His work focused on paths on curved surfaces.

Marston Morse in the 1920s and 1930s gave clear answers to these questions. His work led to something called Morse theory. For example, he showed how the number of "conjugate points" in a path relates to the action.

Why Is This Principle Important?

The action principle is very important because it gives us a different way to think about how things move. Usually, we think about motion at one exact moment in time. For example, Newton's second law says that a force causes an object to accelerate right now.

But the action principle is different. It looks at the whole journey of a system over a period of time. It says:

This idea of knowing the final state to understand the path has caused some debate. Some people thought it meant that nature had a "purpose" or "goal" (called teleology). However, many scientists explain that this is just how the math works out when you set up the problem this way.

Also, in quantum physics, the action principle can be seen as a result of all possible paths interfering with each other. This helps explain why the classical path is the one we observe.

The short story Story of Your Life by Ted Chiang talks about Fermat's Principle (a similar idea for light) and its philosophical meaning. Also, the book The Math Instinct by Keith Devlin has a fun chapter about how animals seem to "do calculus" to find the shortest path.

See also

In Spanish: Principio de mínima acción para niños