Trigonometric function facts for kids
In mathematics, trigonometric functions are special rules that connect the angles inside a right triangle to the lengths of its sides. There are six main trigonometric functions. The three most common ones are sine, cosine, and tangent. The other three are cotangent, secant, and cosecant. These last three are called reciprocal trigonometric functions because they are the inverse of the first three.
| Function Name | Short Form | What it's related to |
| Sine | sin | Related to cosine |
| Cosine | cos | Related to sine |
| Tangent | tan | Sine divided by Cosine |
| Cotangent | cot | Cosine divided by Sine (or 1 divided by Tangent) |
| Secant | sec | 1 divided by Cosine |
| Cosecant | csc | 1 divided by Sine |
Contents
What are Trigonometric Functions?
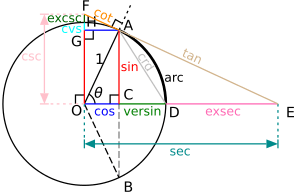
Trigonometric functions are also sometimes called circular functions. They are special functions that use an angle as their input. They are very important when you study triangles and many other areas of math and science.
These functions are usually defined using the sides of a right triangle. A right triangle is a triangle that has one angle that is exactly 90 degrees. You can also think of them as lengths of lines drawn from a unit circle. A unit circle is a circle with a radius of one.
How Right Triangles Define Functions
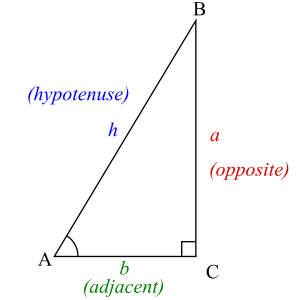
To understand trigonometric functions, let's look at a right triangle. We'll use angle A in our example.
Here are the special names for the sides of a right triangle:
- The hypotenuse is the longest side. It is always the side directly across from the 90-degree angle. We call it h.
- The opposite side is the side directly across from the angle we are interested in (angle A). We call it a.
- The adjacent side is the side next to the angle we are interested in (angle A), but it's not the hypotenuse. It touches both the angle A and the 90-degree angle. We call it b.
In any triangle, all the angles inside add up to 180 degrees. In a right triangle, since one angle is 90 degrees, the other two angles must add up to 90 degrees. This means they are both smaller than 90 degrees.
Let's define the main functions:
1) The sine of an angle is a ratio. It's the length of the opposite side divided by the length of the hypotenuse.
- For angle A: sin A = opposite / hypotenuse = a / h.
- This ratio stays the same for any right triangle that has the same angle A, no matter how big or small the triangle is. This is because all such triangles are similar.
2) The cosine of an angle is also a ratio. It's the length of the adjacent side divided by the length of the hypotenuse.
- For angle A: cos A = adjacent / hypotenuse = b / h.
3) The tangent of an angle is the ratio of the length of the opposite side divided by the length of the adjacent side.
- For angle A: tan A = opposite / adjacent = a / b.
- You can also find the tangent by dividing the sine of the angle by the cosine of the angle.
The next three functions are called reciprocal functions. They are found by flipping the ratios of the first three functions.
4) The cosecant (csc) of an angle is the opposite of sine. It's the length of the hypotenuse divided by the length of the opposite side.
- For angle A: csc A = hypotenuse / opposite = h / a.
5) The secant (sec) of an angle is the opposite of cosine. It's the length of the hypotenuse divided by the length of the adjacent side.
- For angle A: sec A = hypotenuse / adjacent = h / b.
6) The cotangent (cot) of an angle is the opposite of tangent. It's the length of the adjacent side divided by the length of the opposite side.
- For angle A: cot A = adjacent / opposite = b / a.
Important Formulas (Identities)
Here are some important formulas, also called identities, that show how trigonometric functions relate to each other:
- tan x = sin x / cos x
- cot x = cos x / sin x
- sec x = 1 / cos x
- csc x = 1 / sin x
- sin² x + cos² x = 1 (This is the Pythagorean theorem applied to a unit circle!)
Hyperbolic Functions
The hyperbolic functions are similar to trigonometric functions but are based on a different kind of curve called a hyperbola, instead of a circle. They are defined using the exponential function, which involves the special number e (about 2.718). Each of the six trigonometric functions has a matching hyperbolic form.
Related Topics
Images for kids
See also
 In Spanish: Función trigonométrica para niños
In Spanish: Función trigonométrica para niños