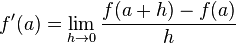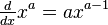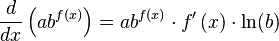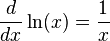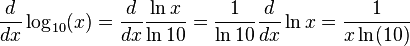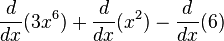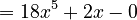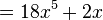Derivative (mathematics) facts for kids
In mathematics, especially in a part called differential calculus, the derivative helps us understand how things change. Think of it like finding the exact speed of a car at one specific moment, not its average speed over a trip.
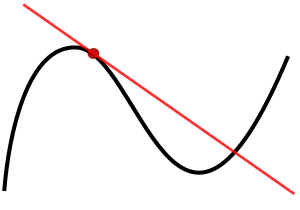
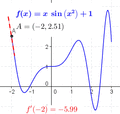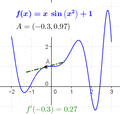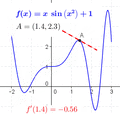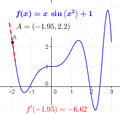
The derivative tells us how much a function is changing at a single point. If you look at a graph, the derivative at a point is the slope of the tangent line that just touches the graph at that point.
You'll often see the derivative written as 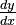 . This means "the change in y divided by the change in x." Another common way to write it is
. This means "the change in y divided by the change in x." Another common way to write it is 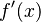 , which means "the derivative of the function
, which means "the derivative of the function 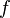 at point
at point 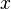 ."
."
Contents
What is a Derivative?
Imagine you have a curve on a graph. If you pick two points on that curve, you can draw a straight line between them. The slope of this line tells you how much the curve changes between those two points.
Now, imagine moving those two points closer and closer together. As they get super close, the line connecting them becomes almost exactly the same as the tangent line that just touches the curve at one point.
The derivative is basically the slope of this tangent line. It's found by making the distance between two points on the graph incredibly small. In math terms, it looks like this:
This formula means that as the distance h between the two x-values gets closer to zero, the slope of the line between them becomes the slope of the tangent line.
Derivatives of Different Functions
Functions can be different types, and each type has a general rule for finding its derivative.
Linear Functions
Linear functions are simple straight lines, like 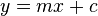 . Here, m is the slope, and c is where the line crosses the y-axis.
. Here, m is the slope, and c is where the line crosses the y-axis.
For a straight line, the slope is always the same everywhere. So, the derivative of a linear function is just its slope.
- If you have
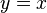 , the slope is 1. So,
, the slope is 1. So, 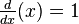 .
. - If you have
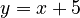 , the line is just shifted up. The slope is still 1. So, its derivative is also 1.
, the line is just shifted up. The slope is still 1. So, its derivative is also 1. - If you have
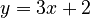 , the slope is 3. So, its derivative is 3.
, the slope is 3. So, its derivative is 3.
Power Functions
Power functions look like 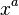 , where a is a number (the exponent). Their slope changes depending on where you are on the graph.
, where a is a number (the exponent). Their slope changes depending on where you are on the graph.
There's a simple rule for power functions:
Let's look at some examples:
- If you have
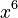 , its derivative is
, its derivative is 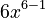 , which is
, which is 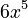 .
. - What about
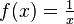 ? This can be written as
? This can be written as 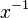 .
.
* Using the rule: 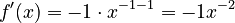 . * This can be written as
. * This can be written as 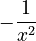 .
.
- Roots can also be written with fractional exponents. For example,
![f(x) = \sqrt[3]{x^2}](/images/math/b/d/c/bdc20273dd42b98199bd0becb33c9917.png) is the same as
is the same as 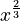 .
.
* Using the rule: 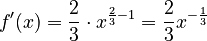 .
.
Exponential Functions
Exponential functions are different because the variable x is in the exponent, like 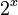 or
or 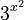 .
.
The general rule for an exponential function 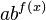 is:
is:
Here, 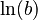 is the natural logarithm of b.
is the natural logarithm of b.
Let's try an example: Find the derivative of 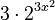 .
.
- Here,
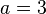 ,
, 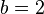 , and
, and 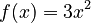 .
. - First, find the derivative of
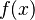 , which is
, which is 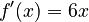 .
. - Now, put it all into the rule:
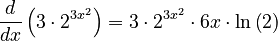 This can be rearranged to:
This can be rearranged to: 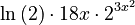
Logarithmic Functions
The derivative of a logarithm is often a reciprocal. The most common logarithm in calculus is the natural logarithm, written as 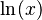 .
.
Example: Find the derivative of 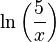 .
.
- Using logarithm rules,
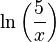 can be split into
can be split into 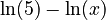 .
. - The derivative of
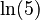 is 0, because
is 0, because 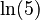 is just a constant number.
is just a constant number. - The derivative of
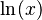 is
is 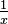 .
. - So, the derivative of
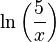 is
is 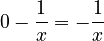 .
.
For logarithms with a different base, like 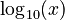 , you can convert them to natural logarithms:
, you can convert them to natural logarithms:
Trigonometric Functions
Trigonometric functions like sine and cosine also have derivatives. These rules apply when angles are measured in radians.
- The derivative of
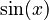 is
is 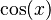 .
.
: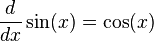
- The derivative of
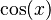 is
is 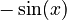 .
.
: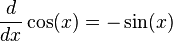
- The derivative of
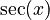 is
is 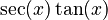 .
.
: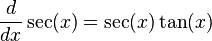
Properties of Derivatives
When you have a function made of several parts, you can often find the derivative of each part separately and then add or subtract them. This makes finding derivatives much easier!
For example, let's find the derivative of 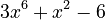 . You can break it down:
. You can break it down:
- The derivative of
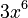 is
is 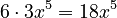 .
. - The derivative of
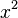 is
is 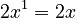 .
. - The derivative of a constant number like 6 is always 0, because constants don't change.
So, the full derivative is:
Uses of Derivatives
Derivatives are super useful in many areas of math and science!
- Finding Maxima and Minima: Imagine a roller coaster track. At the very top of a hill or the very bottom of a valley, the track is momentarily flat. This means its slope (and thus its derivative) is zero. We can use derivatives to find these highest and lowest points of a function.
- Newton's Method: Derivatives help us find where a function crosses the x-axis (its "roots" or "zeros"). This is used in computer programs to solve complex equations.
- Increasing or Decreasing: A derivative can tell you if a function is going up (increasing) or going down (decreasing) at any given point. If the derivative is positive, the function is increasing. If it's negative, the function is decreasing.
Related pages
Images for kids