Surface-area-to-volume ratio facts for kids

Kids Encyclopedia Facts

The surface-area-to-volume ratio (often called SA:V or surface-to-volume ratio) tells us how much surface area an object has compared to its volume (the space it takes up). Think of it as how much "outside" there is for every bit of "inside."

This ratio is super important in science and engineering. It helps explain how things work, especially when processes happen on the surface and spread through the volume. For example, it helps us understand how oxygen and carbon dioxide move between air, blood, and cells. It also explains how animals lose water, how bacteria grow, and how living things control their body temperature. Scientists even use it to design things like artificial bones and lungs!

When an object has a large SA:V, it means there's a lot of surface for its size. This is important for things like diffusion (when tiny particles spread out) or heat transfer (when heat moves). A larger surface means more space for these processes to happen, so they can be much faster. Imagine trying to dissolve a big sugar cube versus tiny sugar grains – the grains dissolve faster because they have more surface area exposed to the water.

For any given amount of space, a ball (like a sphere) has the smallest surface area. This means it has the smallest SA:V. On the other hand, objects with sharp, pointy parts will have a very large surface area for their size.

What is SA:V for a Ball?
How We Measure SA:V
SA:V in Chemistry
SA:V in Biology
SA:V and Wildfires
SA:V and Planetary Cooling
Mathematical Examples
Images for kids
See also

What is SA:V for a Ball?

A ball is a solid, three-dimensional shape, like a soccer ball. In geometry, a sphere usually means just the outer surface, not the solid inside.

This graph shows how the surface-area-to-volume ratio (SA:V) for a 3D ball changes. As the ball gets bigger (its radius increases), the SA:V gets smaller.

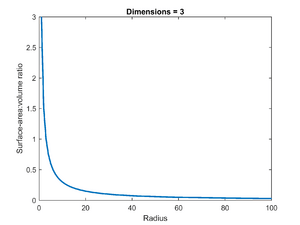
For a regular 3D ball, you can figure out its SA:V using its surface area and volume. If a ball has a radius of 1 unit, its SA:V is 3. The interesting thing is that as a ball gets bigger (its radius increases), its SA:V actually gets smaller. If you double the radius of a ball, its SA:V will be cut in half! This is a key idea: larger objects of the same shape have a smaller SA:V.

How We Measure SA:V

The surface-area-to-volume ratio is measured in units like "per centimeter" (cm⁻¹) or "per meter" (m⁻¹). It's like saying "how many units of surface area for every unit of volume."

Let's look at a cube to understand this:

Imagine a cube with sides that are 1 cm long.
Its surface area is 6 cm² (because it has 6 faces, and each face is 1 cm x 1 cm = 1 cm²).
Its volume is 1 cm³ (1 cm x 1 cm x 1 cm).
So, its SA:V is 6 cm² / 1 cm³ = 6 cm⁻¹.

Now, imagine a bigger cube with sides that are 2 cm long:

Its surface area is 6 x (2 cm x 2 cm) = 6 x 4 cm² = 24 cm².
Its volume is 2 cm x 2 cm x 2 cm = 8 cm³.
Its SA:V is 24 cm² / 8 cm³ = 3 cm⁻¹.

Notice that when the cube got bigger (from 1 cm to 2 cm sides), its SA:V went down from 6 to 3. This shows that for the same shape, a larger object will always have a smaller surface-area-to-volume ratio.

SA:V in Chemistry

The cells that line your small intestine have tiny, finger-like folds called microvilli. These folds greatly increase the surface area, helping your body absorb nutrients from food more effectively.

Materials with a high SA:V react much faster than solid, blocky materials. This is because there's more surface available for chemical reactions to happen.

Here are some examples:

Grain dust: A single grain of wheat isn't very flammable. But if you grind many grains into fine dust, that dust can actually explode! This is because the tiny dust particles have a huge surface area exposed to the air, allowing them to burn very quickly.
Salt: Finely ground salt dissolves much faster in water than coarse salt. Again, more surface area means the water can reach more of the salt at once.

A high SA:V can also speed up other natural processes that try to reach a stable state.

SA:V in Biology

The SA:V of cells and organisms has a huge effect on how they live and function.

Tiny organisms: Many small living things in water have increased surface areas. This helps them float better and not sink, so they don't have to use as much energy to stay near the surface where there's light and food.
Filter feeders: Animals like krill have finely branched parts that act like sieves. These branches have a large surface area to help them filter tiny food particles from the water.
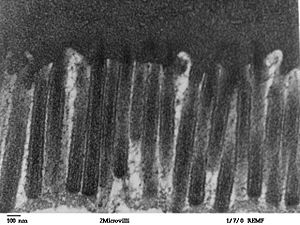
Internal organs: Your lungs have many tiny air sacs that look like branches. This massively increases their surface area, which is perfect for exchanging gases: taking oxygen into your blood and releasing carbon dioxide. Similarly, your small intestine has a very wrinkled inner surface with tiny folds called microvilli. This huge surface area helps your body absorb nutrients from food very efficiently.
Challenges: While a high SA:V can be good, it can also cause problems. More surface area means more contact with the environment, which can lead to losing water or dissolved substances. It also makes it harder for animals to control their body temperature in very hot or cold places. This is why animals in cold climates often have a smaller SA:V (they are more compact) than animals in hot climates.

SA:V and Wildfires

In wildfires, the SA:V of fuel (like leaves and branches) is very important. The higher this ratio, the faster the fuel reacts to changes in the environment, such as temperature or moisture. Fuels with a higher SA:V also catch fire more quickly, which means the fire spreads faster.

SA:V and Planetary Cooling

Graphs showing how surface area (A) changes with volume (V) for different shapes like the Platonic solids and a sphere. It shows that rounder shapes have less surface area for their volume, and as an object gets bigger, its surface-area-to-volume ratio decreases.

Planets and moons in space are made of rock or ice. If they can hold onto enough heat, their insides can change, and their surfaces can be shaped by things like volcanoes or earthquakes. How long a planet can stay active depends on how well it keeps its heat, and this is controlled by its surface-area-to-volume ratio.

Small bodies: For example, Vesta, a large asteroid, is relatively small. It has a high SA:V, meaning it loses heat quickly. Scientists were surprised to find that it once had volcanic activity.
Medium bodies: The moon, Mercury, and Mars are bigger than Vesta but still much smaller than Earth. They kept enough heat to form different layers inside, but after about a billion years, they cooled down too much for much volcanic activity. However, in 2019, a "marsquake" was detected, showing some activity still exists.
Large bodies: Venus and Earth are very large. They have very low SA:V ratios, meaning they lose heat very slowly. This is why they are still geologically active today, with volcanoes and earthquakes.

Mathematical Examples

Here are some examples of SA:V for different shapes:

Shape	Characteristic length a	Surface area	Volume	SA/V ratio
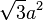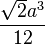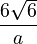Tetrahedron	edge	$\sqrt{3} a^2$	$\frac{\sqrt{2}a^3}{12}$	Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{6\sqrt{6}}{a}
Cube	edge	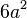$6a^2$	$a^3$	$\frac{6}{a}$
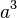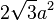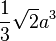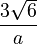Octahedron	edge	$2\sqrt{3}a^2$	$\frac{1}{3} \sqrt{2}a^3$	Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{3\sqrt{6}}{a}
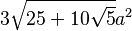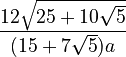Dodecahedron	edge	$3\sqrt{25+10\sqrt{5}} a^2$	$\frac{1}{4} (15+7\sqrt{5}) a^3$	Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{12\sqrt{25+10\sqrt{5}}}{(15+7\sqrt{5})a}
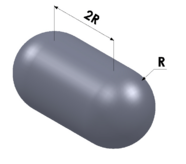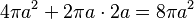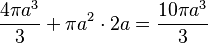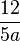Capsule	radius (R)	$4\pi a^2+2\pi a \cdot 2a = 8\pi a^2$	$\frac{4\pi a^3}{3} + \pi a^2 \cdot 2a = \frac{10\pi a^3}{3}$	$\frac{12}{5a}$
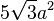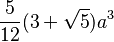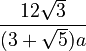Icosahedron	edge	$5\sqrt{3}a^2$	$\frac{5}{12} (3+\sqrt5)a^3$	Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{12 \sqrt{3}}{(3+\sqrt{5})a}
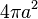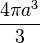Sphere	radius	$4\pi a^2$	$\frac{4\pi a^3}{3}$	$\frac{3}{a}$

Here's how the SA:V changes for cubes of different sizes:

Examples of cubes of different sizes
Side of cube	Area of a single face	Area of entire cube (6 faces)	Volume	Ratio of surface area to volume
2	4	24	8	3:1
4	16	96	64	3:2
6	36	216	216	3:3
8	64	384	512	3:4
12	144	864	1,728	3:6
20	400	2,400	8,000	3:10
50	2,500	15,000	125,000	3:25
1,000	1,000,000	6,000,000	1,000,000,000	3:500

Images for kids

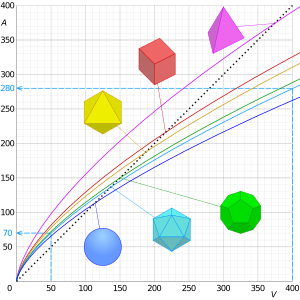
Graphs of surface area, A against volume, V of the Platonic solids and a sphere, showing that the surface area decreases for rounder shapes, and the surface-area-to-volume ratio decreases with increasing volume. Their intercepts with the dashed lines show that when the volume increases 8 (2³) times, the surface area increases 4 (2²) times.
Plot of the surface-area:volume ratio (SA:V) for a 3-dimensional ball, showing the ratio decline inversely as the radius of the ball increases.
Plot of surface-area:volume ratio (SA:V) for n-balls as a function of the number of dimensions and of radius size. Note the linear scaling as a function of dimensionality and the inverse scaling as a function of radius.
Cells lining the small intestine increase the surface area over which they can absorb nutrients with a carpet of tuftlike microvilli.