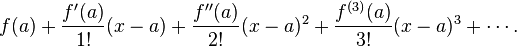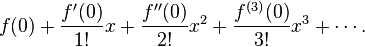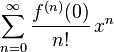Taylor series facts for kids
A Taylor series is a cool idea in mathematics that helps us understand and work with complex math rules, called functions. Think of a function as a rule that takes an input number and gives you an output number. A Taylor series helps us make a really good guess, or estimate, of what a function looks like, especially around a certain point. It's used in many areas like computer science, calculus, physics, and chemistry. There's also a special type of Taylor series called a Maclaurin series.
The main idea behind a Taylor series is that if you pick a point on a graph (like on a coordinate plane with X and Y axes), you can use it to guess how a function behaves nearby. You do this by breaking the function down into many simpler parts, called derivatives, and adding them up. Even though you might add an infinite number of these parts, they can still add up to a single, finite answer.
Contents
What Is a Taylor Series?
In math, a Taylor series shows a function as a sum of an infinite series. This means it's an endless list of numbers added together. Each number in the sum comes from the function's derivatives. Derivatives tell us how a function is changing at any given point. Taylor series are based on something called Taylor's theorem.
History of Taylor Series
The idea of adding up an infinite number of things to get a single answer goes way back to the Ancient Greek philosopher Zeno of Elea. He came up with a famous puzzle called "Zeno's paradoxes". Zeno thought it would be impossible to add an endless number of values and still get a single, limited answer.
Another Greek philosopher, Aristotle, tried to answer Zeno's puzzle. But it was Archimedes who found a mathematical way to solve it. He used his "method of exhaustion" to show that if you split something into an infinite number of tiny pieces, they can still add up to a whole when put back together. A few hundred years later, the ancient Chinese mathematician Liu Hui proved the same thing.
The first known examples of what we now call Taylor series come from Mādhava of Sañgamāgrama in India in the 1300s. Later Indian mathematicians wrote about his work with special math rules called trigonometric functions, like sine, cosine, tangent, and arctangent. Sadly, none of Mādhava's original writings still exist. Other mathematicians built on his discoveries until the 1500s.
In the 1600s, James Gregory, a Scottish mathematician, also worked on these ideas. He studied Taylor series and published some Maclaurin series. Then, in 1715, Brook Taylor found a general way to use these series for all kinds of functions. Before him, the methods only worked for specific functions. Later, in the 1700s, Colin Maclaurin published a special version of the Taylor series. This version, which is centered around the number zero, is now called the Maclaurin series.
How Taylor Series Are Defined
A Taylor series can describe any function ƒ(x) that is "smooth" (meaning you can take its derivative an infinite number of times). The function ƒ can use either real numbers or complex numbers. The Taylor series then helps describe what the function looks like very close to a specific number a.
This Taylor series, written as a power series (a series where each term has a higher power of x), looks like this:
You can also write this formula using a special math symbol called sigma notation:
In these formulas:
- n! means the factorial of n (for example, 3! = 3 × 2 × 1 = 6).
- ƒ (n)(a) means the nth derivative of ƒ at the point a.
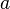is a number that the function can use.
If a function's Taylor series is exactly equal to that function, the function is called an "analytic function."
What Is a Maclaurin Series?
When the number 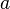in the Taylor series is set to zero (
), the series is called a Maclaurin series. It's a special, simpler case of the Taylor series.
The Maclaurin series written as a power series looks like this:
When written in sigma notation, the Maclaurin series is:
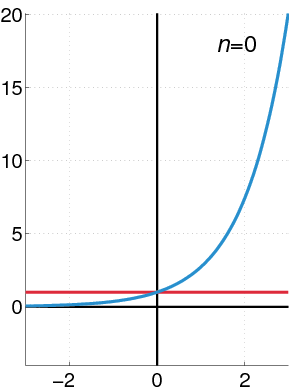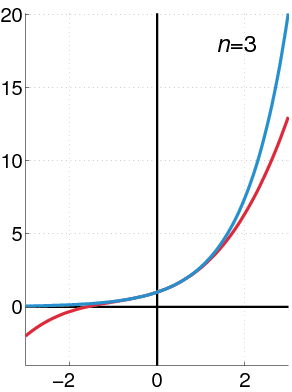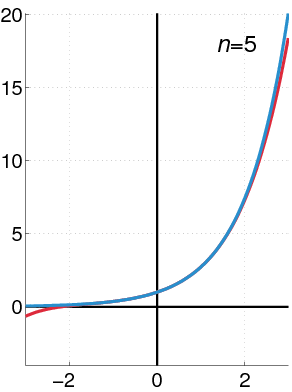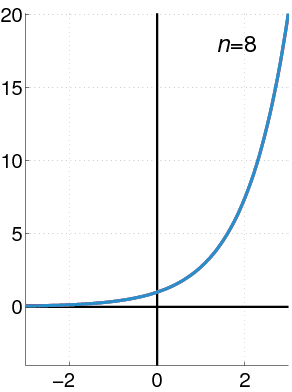
Examples of Taylor Series
Here are some important Taylor series and Maclaurin series for common math functions:
- Sine function (
):
:Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots\text{ for all } x\!
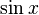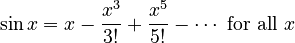
- Cosine function (
):
:Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots\text{ for all } x\!
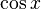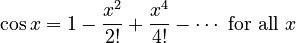
- Exponential function (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^{x} ):
:Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): e^{x} = 1 + x + \frac{1}{2!} x^{2} + \frac{1}{3!} x^{3} + \cdots\text{ for all } x \!
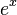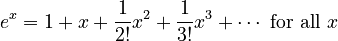
- Geometric series (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{1-x} ):
:Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{1-x} = 1 + x + x^2 + x^3 + x^4 + \cdots \text{ for all } |x|<1
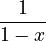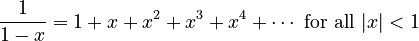
- Natural logarithm (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \ln(1+x) ):
:Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots \text { for all } |x|<1
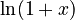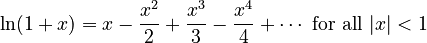
- Tangent function (
):
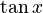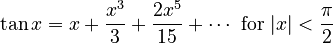:Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tan x = x + \frac{x^3}{3} + \frac{2 x^5}{15} + \cdots\text{ for }|x| < \frac{\pi}{2}\! pl:Wzór Taylora#Szereg Taylora
See also
In Spanish: Serie de Taylor para niños
