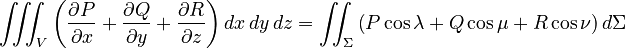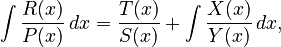Mikhail Ostrogradsky facts for kids
Quick facts for kids
Mikhail Ostrogradsky
|
|
|---|---|
Mikhail Vasilyevich Ostrogradsky
|
|
| Born | 24 September 1801 Pashennaya, Kobelyaksky Uyezd, Poltava Governorate, Russian Empire; now Kremenchuk Raion, Poltava Oblast, Ukraine
|
| Died | 1 January 1862 (aged 60) Poltava
|
| Citizenship | Russian Empire |
| Alma mater | University of Kharkiv, University of Paris |
| Known for | Ostrogradsky instability, Divergence theorem |
| Scientific career | |
| Fields | Mathematics |
Mikhail Vasilyevich Ostrogradsky (born September 24, 1801 – died January 1, 1862) was a brilliant Ukrainian mathematician, expert in mechanics, and physicist. He came from a family of Ukrainian Cossacks. Ostrogradsky was a student of Timofei Osipovsky. Many people also see him as a follower of Leonhard Euler, who was a very important mathematician in the Russian Empire.
Contents
A Life of Learning
Mikhail Ostrogradsky was born on September 24, 1801, in a village called Pashennaya. This village was in what is now Ukraine. From 1816 to 1820, he studied at the Imperial University of Kharkov under a teacher named Timofei Osipovsky.
However, in 1820, his teacher Osipovsky was suspended from the university. Because of this, Ostrogradsky refused to take his final exams. This meant he never officially received his Ph.D. degree.
From 1822 to 1826, Ostrogradsky continued his studies in Paris, France. He attended famous schools like the Sorbonne and the Collège de France.
In 1828, he returned to the Russian Empire and settled in Saint Petersburg. There, he was chosen to be a member of the Academy of Sciences. He also became a professor at the main military engineering school in the Russian Empire.
Ostrogradsky passed away in Poltava in 1862 when he was 60 years old. Today, the Kremenchuk Mykhailo Ostrohradskyi National University in Kremenchuk and a street in Poltava are named after him.
His Important Work
Ostrogradsky worked on many different areas of mathematics. These included calculus of variations (which deals with finding the best way to do things), integrating complex functions, number theory (the study of numbers), algebra, geometry, and probability theory (the study of chance).
He also made big contributions to applied mathematics, mathematical physics, and classical mechanics. In mechanics, he helped understand how elastic bodies move. He also developed new ways to solve equations related to motion and fluid power (how liquids and gases move). He built on the work of other famous mathematicians like Euler and Joseph Louis Lagrange.
In Russia, other mathematicians like Nikolay Dmitrievich Brashman and Nikolai Yegorovich Zhukovsky continued his work.
Interestingly, Ostrogradsky did not like the new ideas about non-Euclidean geometry that Nikolai Lobachevsky proposed in 1823. He even rejected Lobachevsky's work when it was submitted for publication.
Ostrogradsky was also a teacher to the children of Emperor Nicholas I.
The Divergence Theorem
In 1826, Ostrogradsky was the first to prove a very important rule in mathematics called the divergence theorem. This theorem was first thought of by Lagrange in 1762.
This theorem helps us understand the relationship between a flow (like water or air) inside a space and the flow going out through the surface of that space. It's often used in physics and engineering.
The theorem can be written using Ostrogradsky's equation:
This equation might look complicated, but it basically says that if you add up how much something is spreading out (or "diverging") inside a 3D space (V), it's the same as adding up how much of that something is flowing out through the surface (Σ) that surrounds the space.
Ostrogradsky's Integration Method
Ostrogradsky also developed a well-known method for integrating certain types of mathematical functions called rational functions. These are functions that look like fractions, with one polynomial divided by another.
His method helps mathematicians break down a complex integral into two parts:
- A "rational part" which is an algebraic fraction.
- A "transcendental part" which might involve things like logarithms or arctangents.
The cool thing about his method is that it helps you find the rational part of the integral without having to do the full integration first! He gave a specific form for this:
This method makes solving some tough integration problems much easier for mathematicians.
See also
- Gauss-Ostrogradsky theorem
- Green's theorem
- Ostrogradsky instability
Images for kids
-
A 2 hryvna commemorative coin minted by the National Bank of Ukraine in 2001.
-
Commemorative plaque in Poltava on the last house where Ostrogradsky resided.
-
Ostrogradsky's grave in the village of Pashenivka, where he was born.
