Modulo facts for kids

Kids Encyclopedia Facts

This page is about the binary operation mod( $a,n$ ). For the (mod $n$ ) notation, see Modular arithmetic. For other uses, see Modulo (disambiguation).

In computing, the modulo operation helps us find the remainder when one number is divided by another. Think of it like this: if you have 5 cookies and you divide them among 2 friends, each friend gets 2 cookies, and you have 1 cookie left over. That "1" is the remainder, and that's what the modulo operation gives you! The number you divide by is called the modulus.

When we have two positive numbers, let's say a and n, a modulo n (often written as a mod n) is the leftover part after you divide a by n. Here, a is the number being divided (the dividend), and n is the number you're dividing by (the divisor).

For example, "5 mod 2" equals 1. Why? Because 5 divided by 2 is 2 with a remainder of 1. If you see "9 mod 3", the answer is 0. This is because 9 divided by 3 is exactly 3, with no remainder left.

Usually, we use whole numbers for modulo operations. However, many computer systems can now use other types of numbers too. When you do a modulo operation with a number n, the result will always be a whole number between 0 and n − 1. For instance, a mod 1 is always 0. But be careful: a mod 0 is usually not allowed and can cause an error in computer programs!

Things get a bit tricky when one of the numbers (a or n) is negative. Different programming languages handle these situations in different ways.

How the Modulo Operation Works Differently
How We Write Modulo Operations
Common Mistakes with Modulo
Making Modulo Operations Faster
Properties of Modulo Operations
Modulo in Programming Languages
Images for kids

How the Modulo Operation Works Differently

In mathematics, the result of a modulo operation is part of a group of numbers that are all "the same" in a special way. We usually pick the smallest non-negative number from this group as the answer. But computers and calculators can define the modulo operation in various ways, depending on the programming language or the computer's parts.

Almost all computer systems follow these rules for division:

Both the quotient (the result of the division) and the remainder must be whole numbers.
The original number a must equal the divisor n multiplied by the quotient q, plus the remainder r. So, a = n q + r.
The absolute value (size) of the remainder must be smaller than the absolute value of the divisor.

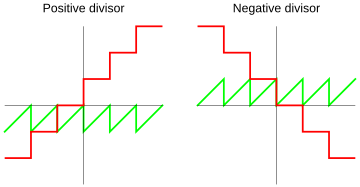
However, if the remainder isn't zero, there's still a choice to make: should the remainder be positive or negative? In math, we always choose a positive remainder. But in computing, programming languages decide based on the signs of a or n. For example, some languages like Pascal always give a positive remainder, even if you divide by a negative number. Other languages, like C90, let the computer decide what happens when n or a is negative. Dividing by 0 is usually not allowed in most systems.

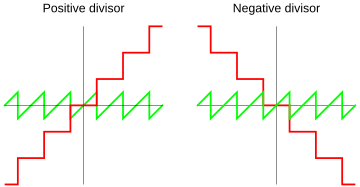
Here are some common ways computers define how to find the quotient and remainder:

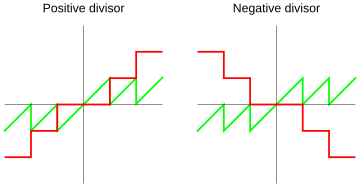
Truncated Division:

This method rounds the quotient (the result of the division) towards zero.

The quotient and remainder when using truncated division.

With this method, the remainder will always have the same sign as the number being divided (the dividend).

Floored Division:

Donald Knuth, a famous computer scientist, prefers this method. Here, the quotient is always rounded down to the nearest whole number.

The quotient and remainder when using floored division.

With this method, the remainder will always have the same sign as the number you're dividing by (the divisor).

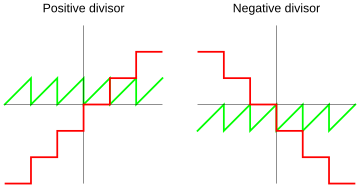
Euclidean Division:

This method is promoted by Raymond T. Boute. It's designed so that the remainder is always non-negative (0 or positive).

The quotient and remainder when using Euclidean division.

Rounded Division:

Some languages like Common Lisp and IEEE 754 use this. The quotient is rounded to the nearest whole number.

The quotient and remainder when using rounded division.

With this method, the remainder will be between negative half of n and positive half of n. Its sign depends on which side of zero it falls.

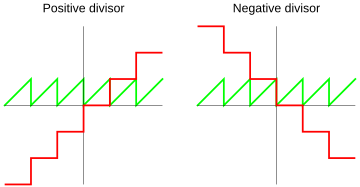
Ceiling Division:

Common Lisp also uses this. The quotient is always rounded up to the nearest whole number.

The quotient and remainder when using ceiling division.

With this method, the remainder will have the opposite sign of the divisor.

Experts like Daan Leijen say that Euclidean division is often the best because it's very consistent and has useful math properties. Floored division is also considered good. Even though truncated division is used a lot, it's often seen as less ideal than the others.

How We Write Modulo Operations

Many calculators have a special button or function called `mod()` or `MOD()`. In programming languages, you might see it written as `mod(a, n)`. Some languages also use symbols like "%", "mod", or "Mod" as an operator, for example, `a % n` or `a mod n`.

If a programming environment doesn't have a built-in modulo function, programmers can create one using the division methods we talked about earlier.

Common Mistakes with Modulo

When the result of a modulo operation has the same sign as the number being divided (like in truncated division), it can sometimes lead to unexpected errors.

For example, imagine you want to check if a number is odd. You might think you can just check if the remainder when divided by 2 is 1:

bool is_odd(int n) {
    return n % 2 == 1;
}

But this can be wrong! If n is a negative odd number, like -5, and the modulo operation gives the same sign as the dividend (truncated definition), then -5 mod 2 would be -1, not 1. In this case, the function would incorrectly say that -5 is not odd.

A better way to check if a number is odd is to see if the remainder is not 0. This works because a remainder of 0 is always 0, no matter the signs:

bool is_odd(int n) {
    return n % 2 != 0;
}

Another way is to check if the remainder is either 1 or -1 (since odd numbers will always have one of these remainders when divided by 2):

bool is_odd(int n) {
    return n % 2 == 1 || n % 2 == -1;
}

Or, even simpler, you can often just use the result of `n % 2` as a true/false value, where any non-zero value means "true":

bool is_odd(int n) {
    return n % 2;
}

Making Modulo Operations Faster

Sometimes, computers calculate modulo by doing a full division first. But for special cases, there are faster ways! For example, if you need to find the modulo of a number by a powers of 2 (like 2, 4, 8, 16, etc.), you can use a bitwise AND operation. This is much quicker on some computer hardware.

For a positive whole number x, and a power of 2 (like 2ⁿ), this works: `x % 2ⁿ == x & (2ⁿ - 1)`

Here are some examples:

`x % 2 == x & 1`
`x % 4 == x & 3`
`x % 8 == x & 7`

If a computer or software can do bitwise operations faster than modulo, these alternative forms will make calculations quicker.

Special programs called compilers can sometimes automatically change your code to use these faster bitwise operations if they see you're doing a modulo by a power of two. This means you can write clear code, and the computer will still make it run fast! However, this trick doesn't always work if the number you're dividing (the dividend) can be negative, unless it's an unsigned integer (a number that can only be positive).

Properties of Modulo Operations

Just like other math operations, modulo operations have special rules and properties. These can be very useful in cryptography (like for secure communication). These rules usually apply when a and n are whole numbers.

Identity:
- (a mod n) mod n = a mod n (Doing modulo twice by the same number doesn't change the result).
- n^x mod n = 0 (If you raise n to any positive whole number power and then modulo by n, the remainder is 0).
Inverse:
- [(-a mod n) + (a mod n)] mod n = 0 (Adding a number's negative modulo to its positive modulo gives 0).
Distributive:
- (a + b) mod n = [(a mod n) + (b mod n)] mod n (You can add first, then modulo, or modulo each number then add, then modulo again).
- ab mod n = [(a mod n)(b mod n)] mod n (You can multiply first, then modulo, or modulo each number then multiply, then modulo again).

Modulo in Programming Languages

Different programming languages handle the modulo operation in various ways, especially when dealing with negative numbers or decimals. The table below shows how some popular languages define their modulo or remainder operators.

Modulo operators in various programming languages
Language	Operator	Whole Numbers	Decimal Numbers	Definition
ABAP	`MOD`	Yes	Yes	Euclidean
ActionScript	`%`	Yes	No	Truncated
Ada	`mod`	Yes	No	Floored
Ada	`rem`	Yes	No	Truncated
ALGOL 68	`÷×`, `mod`	Yes	No	Euclidean
AMPL	`mod`	Yes	No	Truncated
APL	`\|`	Yes	No	Floored
AppleScript	`mod`	Yes	No	Truncated
AutoLISP	`(rem d n)`	Yes	No	Truncated
AWK	`%`	Yes	No	Truncated
bash	`%`	Yes	No	Truncated
BASIC	`Mod`	Yes	No	Undefined
bc	`%`	Yes	No	Truncated
C C++	`%`, `div`	Yes	No	Truncated
	`fmod` (C) `std::fmod` (C++)	No	Yes	Truncated
	`remainder` (C) `std::remainder` (C++)	No	Yes	Rounded
C#	`%`	Yes	Yes	Truncated
C#	`Math.IEEERemainder`	No	Yes	Rounded
Clarion	`%`	Yes	No	Truncated
Clean	`rem`	Yes	No	Truncated
Clojure	`mod`	Yes	No	Floored
Clojure	`rem`	Yes	No	Truncated
COBOL	`FUNCTION MOD`	Yes	No	Floored
CoffeeScript	`%`	Yes	No	Truncated
CoffeeScript	`%%`	Yes	No	Floored
ColdFusion	`%`, `MOD`	Yes	No	Truncated
Common Lisp	`mod`	Yes	Yes	Floored
Common Lisp	`rem`	Yes	Yes	Truncated
Crystal	`%`, `modulo`	Yes	Yes	Floored
Crystal	`remainder`	Yes	Yes	Truncated
D	`%`	Yes	Yes	Truncated
Dart	`%`	Yes	Yes	Euclidean
Dart	`remainder()`	Yes	Yes	Truncated
Eiffel	`\\`	Yes	No	Truncated
Elixir	`rem/2`	Yes	No	Truncated
Elixir	`Integer.mod/2`	Yes	No	Floored
Elm	`modBy`	Yes	No	Floored
Elm	`remainderBy`	Yes	No	Truncated
Erlang	`rem`	Yes	No	Truncated
Erlang	`math:fmod/2`	No	Yes	Truncated (same as C)
Euphoria	`mod`	Yes	No	Floored
Euphoria	`remainder`	Yes	No	Truncated
F#	`%`	Yes	Yes	Truncated
F#	`Math.IEEERemainder`	No	Yes	Rounded
Factor	`mod`	Yes	No	Truncated
FileMaker	`Mod`	Yes	No	Floored
Forth	`mod`	Yes	No	Implementation defined
	`fm/mod`	Yes	No	Floored
	`sm/rem`	Yes	No	Truncated
Fortran	`mod`	Yes	Yes	Truncated
Fortran	`modulo`	Yes	Yes	Floored
Frink	`mod`	Yes	No	Floored
GLSL	`%`	Yes	No	Undefined
GLSL	`mod`	No	Yes	Floored
GameMaker Studio (GML)	`mod`, `%`	Yes	No	Truncated
GDScript (Godot)	`%`	Yes	No	Truncated
	`fmod`	No	Yes	Truncated
	`posmod`	Yes	No	Floored
	`fposmod`	No	Yes	Floored
Go	`%`	Yes	No	Truncated
	`math.Mod`	No	Yes	Truncated
	`big.Int.Mod`	Yes	No	Euclidean
Groovy	`%`	Yes	No	Truncated
Haskell	`mod`	Yes	No	Floored
	`rem`	Yes	No	Truncated
	`Data.Fixed.mod'` (GHC)	No	Yes	Floored
Haxe	`%`	Yes	No	Truncated
HLSL	`%`	Yes	Yes	Undefined
J	`\|`	Yes	No	Floored
Java	`%`	Yes	Yes	Truncated
Java	`Math.floorMod`	Yes	No	Floored
JavaScript TypeScript	`%`	Yes	Yes	Truncated
Julia	`mod`	Yes	Yes	Floored
Julia	`%`, `rem`	Yes	Yes	Truncated
Kotlin	`%`, `rem`	Yes	Yes	Truncated
Kotlin	`mod`	Yes	Yes	Floored
ksh	`%`	Yes	No	Truncated (same as POSIX sh)
ksh	`fmod`	No	Yes	Truncated
LabVIEW	`mod`	Yes	Yes	Truncated
LibreOffice	`=MOD()`	Yes	No	Floored
Logo	`MODULO`	Yes	No	Floored
Logo	`REMAINDER`	Yes	No	Truncated
Lua 5	`%`	Yes	Yes	Floored
Lua 4	`mod(x,y)`	Yes	Yes	Truncated
Liberty BASIC	`MOD`	Yes	No	Truncated
Mathcad	`mod(x,y)`	Yes	No	Floored
Maple	`e mod m` (by default), `modp(e, m)`	Yes	No	Euclidean
	`mods(e, m)`	Yes	No	Rounded
	`frem(e, m)`	Yes	Yes	Rounded
Mathematica	`Mod[a, b]`	Yes	No	Floored
MATLAB	`mod`	Yes	No	Floored
MATLAB	`rem`	Yes	No	Truncated
Maxima	`mod`	Yes	No	Floored
Maxima	`remainder`	Yes	No	Truncated
Maya Embedded Language	`%`	Yes	No	Truncated
Microsoft Excel	`=MOD()`	Yes	Yes	Floored
Minitab	`MOD`	Yes	No	Floored
Modula-2	`MOD`	Yes	No	Floored
Modula-2	`REM`	Yes	No	Truncated
MUMPS	`#`	Yes	No	Floored
Netwide Assembler (NASM, NASMX)	`%`, `div` (unsigned)	Yes	No	N/A
Netwide Assembler (NASM, NASMX)	`%%` (signed)	Yes	No	Implementation-defined
Nim	`mod`	Yes	No	Truncated
Oberon	`MOD`	Yes	No	Floored-like
Objective-C	`%`	Yes	No	Truncated (same as C99)
Object Pascal, Delphi	`mod`	Yes	No	Truncated
OCaml	`mod`	Yes	No	Truncated
OCaml	`mod_float`	No	Yes	Truncated
Occam	`\`	Yes	No	Truncated
Pascal (ISO-7185 and -10206)	`mod`	Yes	No	Euclidean-like
Programming Code Advanced (PCA)	`\`	Yes	No	Undefined
Perl	`%`	Yes	No	Floored
Perl	`POSIX::fmod`	No	Yes	Truncated
Phix	`mod`	Yes	No	Floored
Phix	`remainder`	Yes	No	Truncated
PHP	`%`	Yes	No	Truncated
PHP	`fmod`	No	Yes	Truncated
PIC BASIC Pro	`\\`	Yes	No	Truncated
PL/I	`mod`	Yes	No	Floored (ANSI PL/I)
PowerShell	`%`	Yes	No	Truncated
Programming Code (PRC)	`MATH.OP - 'MOD; (\)'`	Yes	No	Undefined
Progress	`modulo`	Yes	No	Truncated
Prolog (ISO 1995)	`mod`	Yes	No	Floored
Prolog (ISO 1995)	`rem`	Yes	No	Truncated
PureBasic	`%`, `Mod(x,y)`	Yes	No	Truncated
PureScript	`mod`	Yes	No	Euclidean
Pure Data	`%`	Yes	No	Truncated (same as C)
Pure Data	`mod`	Yes	No	Floored
Python	`%`	Yes	Yes	Floored
Python	`math.fmod`	No	Yes	Truncated
Q#	`%`	Yes	No	Truncated
R	`%%`	Yes	Yes	Floored
Racket	`modulo`	Yes	No	Floored
Racket	`remainder`	Yes	No	Truncated
Raku	`%`	No	Yes	Floored
RealBasic	`MOD`	Yes	No	Truncated
Reason	`mod`	Yes	No	Truncated
Rexx	`//`	Yes	Yes	Truncated
RPG	`%REM`	Yes	No	Truncated
Ruby	`%`, `modulo()`	Yes	Yes	Floored
Ruby	`remainder()`	Yes	Yes	Truncated
Rust	`%`	Yes	Yes	Truncated
Rust	`rem_euclid()`	Yes	Yes	Euclidean
SAS	`MOD`	Yes	No	Truncated
Scala	`%`	Yes	No	Truncated
Scheme	`modulo`	Yes	No	Floored
Scheme	`remainder`	Yes	No	Truncated
Scheme R⁶RS	`mod`	Yes	No	Euclidean
	`mod0`	Yes	No	Rounded
	`flmod`	No	Yes	Euclidean
	`flmod0`	No	Yes	Rounded
Scratch	`mod`	Yes	Yes	Floored
Seed7	`mod`	Yes	Yes	Floored
Seed7	`rem`	Yes	Yes	Truncated
SenseTalk	`modulo`	Yes	No	Floored
SenseTalk	`rem`	Yes	No	Truncated
`sh` (POSIX) (includes bash, mksh, &c.)	`%`	Yes	No	Truncated (same as C)
Smalltalk	`\\`	Yes	No	Floored
Smalltalk	`rem:`	Yes	No	Truncated
Snap!	`mod`	Yes	No	Floored
Spin	`//`	Yes	No	Floored
Solidity	`%`	Yes	No	Floored
SQL (SQL:1999)	`mod(x,y)`	Yes	No	Truncated
SQL (SQL:2011)	`%`	Yes	No	Truncated
Standard ML	`mod`	Yes	No	Floored
	`Int.rem`	Yes	No	Truncated
	`Real.rem`	No	Yes	Truncated
Stata	`mod(x,y)`	Yes	No	Euclidean
Swift	`%`	Yes	No	Truncated
	`remainder(dividingBy:)`	No	Yes	Rounded
	`truncatingRemainder(dividingBy:)`	No	Yes	Truncated
Tcl	`%`	Yes	No	Floored
tcsh	`%`	No	No	Truncated
Torque	`%`	Yes	No	Truncated
Turing	`mod`	Yes	No	Floored
Verilog (2001)	`%`	Yes	No	Truncated
VHDL	`mod`	Yes	No	Floored
VHDL	`rem`	Yes	No	Truncated
VimL	`%`	Yes	No	Truncated
Visual Basic	`Mod`	Yes	No	Truncated
WebAssembly	`i32.rem_u`, `i64.rem_u` (unsigned)	Yes	No	N/A
WebAssembly	`i32.rem_s`, `i64.rem_s` (signed)	Yes	No	Truncated
x86 assembly	`IDIV`	Yes	No	Truncated
XBase++	`%`	Yes	Yes	Truncated
XBase++	`Mod()`	Yes	Yes	Floored
Zig	`%`, `@mod`, `@rem`	Yes	Yes	Truncated
Z3 theorem prover	`div`, `mod`	Yes	No	Euclidean

Many computer systems also offer a `divmod` function. This function gives you both the quotient (the result of the division) and the remainder at the same time. Examples include the `IDIV` instruction in x86 architecture and the `divmod()` function in Python.

Images for kids

The quotient and remainder when using truncated division.
The quotient and remainder when using floored division.
The quotient and remainder when using Euclidean division.
The quotient and remainder when using rounded division.
The quotient and remainder when using ceiling division.

All content from Kiddle encyclopedia articles (including the article images and facts) can be freely used under Attribution-ShareAlike license, unless stated otherwise. Cite this article:

Modulo Facts for Kids. Kiddle Encyclopedia.