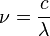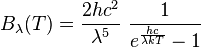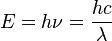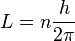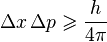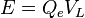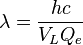Planck constant facts for kids

Kids Encyclopedia Facts

The Planck constant (also called Planck's constant) is a very important number in physics. It connects how much energy a tiny packet of light (called a photon) has with the frequency of its wave. Think of it like a special key that links the wave-like and particle-like sides of light!

This constant is named after the famous physicist Max Planck. It's a fundamental physical constant, which means it's a basic number that helps describe how the universe works. We write it using the letter h.

In the SI system, the Planck constant is exactly 6.62607015×10⁻³⁴ joule-seconds (J·s). Scientists use this number to figure out other important measurements, like the Planck length and the Planck time.

What is the Planck Constant?
Light: Waves or Particles?
How the Planck Constant is Used
The Planck Constant and the Kilogram
Images for kids
Related pages
See also

What is the Planck Constant?

The Planck constant (h) is a tiny number that helps us understand the world at a very small scale, called the quantum level. It shows that energy doesn't come in any amount, but in specific, small packets called "quanta."

Imagine you have a staircase. You can only stand on the steps, not in between them. Energy is similar at the quantum level; it comes in fixed "steps" or packets. The Planck constant tells us the size of these energy steps.

Light: Waves or Particles?

For a long time, scientists argued about what light really was. Was it made of tiny particles, or was it a wave, like ripples in water?

Early Ideas About Light

Back in 1678, a scientist named Christiaan Huygens thought light was made of waves. He said that if light were particles, two beams of light would bounce off each other, but they don't.

However, in 1672, Isaac Newton believed light was made of tiny particles, which he called "corpuscles." He showed how a prism could split white light into different colors and then put them back together. For many years, Newton's particle idea was more popular.

The Wave Theory Takes Over

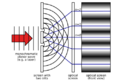
Then, in 1803, Thomas Young did a famous experiment called the "double-slit experiment." He shined light through two tiny slits, and it created a pattern that could only happen if light was behaving like waves. This experiment strongly supported the idea that light was a wave.

Later, in the 1860s, James Clerk Maxwell developed equations that showed light, radio waves, and microwaves were all types of electromagnetic waves. They all travel at the speed of light in a vacuum, but they have different wavelengths. For example, the light we see has wavelengths between 400 and 600 nanometers.

The frequency of an electromagnetic wave (how many waves pass a point per second) is connected to its speed and wavelength by this formula:

\nu = \frac{c}{\lambda}

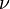Here, $\nu$ is frequency, $c$ is the speed of light, and $\lambda$ is wavelength.

Black Body Radiators

Everything that is warm gives off thermal radiation, which is a type of electromagnetic wave. Very hot things, like a glowing piece of metal, give off visible light. Scientists in the late 1800s studied how much radiation "black-body radiators" (perfect absorbers and emitters of radiation) gave off at different temperatures.

The Ultraviolet Catastrophe

Scientists tried to explain this radiation using existing theories. Lord Rayleigh and Sir James Jeans came up with a formula called the Rayleigh-Jeans law. It worked well for long wavelengths, but it completely failed for short wavelengths (like ultraviolet light). It predicted that a black body would give off an infinite amount of ultraviolet energy, which clearly wasn't true! This problem was famously called the "the ultra-violet catastrophe."

Planck's Solution

In 1900, Max Planck found a way to solve this problem. He suggested that energy from a black body wasn't given off continuously, but in tiny, separate packets, or "quanta." He developed a new formula that matched the experimental results perfectly:

B_\lambda(T) = \frac{2 h c^2}{\lambda^5}~\frac{1}{e^\frac{hc}{\lambda kT}-1}

In this formula, h is the Planck constant and k is the Boltzmann constant.

Planck's idea was revolutionary. It meant that energy, at a very small level, is "quantized" – it comes in specific, discrete amounts. He calculated the value of h to be very close to what we know today.

Light as Particles: The Photoelectric Effect

Even after Planck's discovery, the full meaning of his idea wasn't clear until later. In 1905, Albert Einstein used Planck's constant to explain the photoelectric effect. This is when light hits a metal and makes electrons jump off.

Einstein said that light isn't just a wave; it's also made of tiny particles called photons. Each photon carries a specific amount of energy. If a photon hits an electron, it can knock it off the metal, but only if the photon has enough energy. If the light's frequency is too low, the photons don't have enough energy, and no electrons are released, no matter how bright the light is.

Einstein showed that the energy of each photon is directly related to its frequency by the Planck constant:

E = h\nu = \frac {hc} {\lambda}

Here, E is energy, h is the Planck constant, 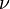$\nu$ is frequency, c is the speed of light, and $\lambda$ is wavelength.

This idea showed that light has both wave-like and particle-like properties, a concept called Wave–particle duality. Max Planck won the Nobel Prize in 1918 for his discovery of energy quanta, and Albert Einstein won the Nobel Prize in 1921 for explaining the photoelectric effect using Planck's constant.

How the Planck Constant is Used

The Planck constant is super important in many areas of physics. Here are a few examples:

Bohr Model of the Atom

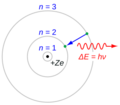
In 1913, Niels Bohr used the Planck constant to create his model of the atom. He said that electrons orbit the nucleus in specific paths, or "energy levels." Electrons can only have certain amounts of energy, and these amounts are related to the Planck constant.

When an electron moves from a higher energy level to a lower one, it gives off a photon of light. Because the energy levels are fixed, the photons released have very specific energies and colors. This is why each chemical element gives off its own unique pattern of colors when heated, like the bright glow of neon lights.

The angular momentum of an electron in an atom is given by:

L=n\frac{h}{2\pi}

Here, L is angular momentum, n is a positive whole number, and h is the Planck constant.

Heisenberg's Uncertainty Principle

In 1927, Werner Heisenberg discovered the uncertainty principle. This principle says that you can't perfectly know both the position and the momentum (how much it's moving) of a tiny particle at the same time. The more accurately you measure one, the less accurately you can know the other.

In our everyday world, when you measure something, you might disturb it a little, but it's usually not a big deal. However, in the quantum world, these disturbances are very important. The Planck constant sets the fundamental limit on how precisely we can measure these properties.

The equation for the uncertainty principle is:

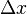\Delta x \, \Delta p\geqslant \frac{h}{4 \pi}\qquad\qquad\qquad

Here, $\Delta x$ is the uncertainty in position, 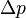$\Delta p$ is the uncertainty in momentum, and h is the Planck constant.

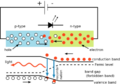
Colors of Light-Emitting Diodes (LEDs)

The Planck constant also helps us understand how LEDs (the small lights in many electronics) produce different colors.

When electricity flows through an LED, electrons jump across a small gap inside the material. When they fall back down, they release energy as light. The color of the light depends on how much energy the electrons lose, which is related to the voltage across the LED.

The energy needed for an electron to jump is:

E = Q_eV_L \,

Here, Q_e is the charge of one electron, and V_L is the voltage across the LED.

Since the energy of the emitted photon is 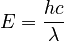Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): E = \frac {hc} {\lambda} , we can combine these to find the wavelength (color) of the light:

\lambda = \frac {hc} {V_L Q_e} \,

This equation shows why different LEDs produce different colors based on their voltage drop.

Colour	Wavelength (nm)	Voltage
red light	650	1.89
green light	550	2.25
blue light	470	2.62

The Planck Constant and the Kilogram

Scientists can measure the Planck constant with incredible accuracy. This high precision has led to a big change in how we define the kilogram.

Before 2019, the kilogram was defined by a physical object, a metal cylinder kept in France. But now, the kilogram is defined using the exact value of the Planck constant! This means that the kilogram is now based on a fundamental constant of nature, making it much more stable and precise.

The reduced Planck constant (ħ) is another value sometimes used in quantum mechanics. It is defined as:

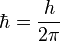\hbar = \frac{h}{2 \pi}

Images for kids

Illustration from Newton's original letter showing how a prism splits sunlight into colors.
Young's double slit experiment, showing light interfering like waves.
Famous photo from the 1911 Solvay Conference, with Max Planck and Albert Einstein.
Bohr's model of the atom, showing an electron moving between energy levels and emitting a photon.
The unique pattern of colors given off by neon gas.
A simple LED circuit, showing how the color of light depends on voltage.