Algebra facts for kids

Kids Encyclopedia Facts

Algebra is a part of mathematics. People often call it math or maths. It helps us solve problems using variables. A variable is a symbol, usually a letter like x or y, that stands for a number we don't know yet.

When we use an equals sign (=), it's called an equation. For example, in the equation 2 + 3 = x, the variable x stands for the number 5. We say we are "solving for x". Algebra also deals with inequalities, which show if something is less than or greater than something else. A special kind of equation is a function. Functions are great for making graphs because they always turn one input into one specific output.

Algebra is super useful for solving real-world problems. Its rules work in everyday life, and numbers can represent real things. Fields like Physics, engineering, and computer programming use algebra all the time. It's also helpful in surveying, construction, and business, especially accounting.

People who use algebra follow rules for numbers and mathematical operations. The simplest operations are adding, subtracting, multiplying, and dividing. More advanced operations include exponents, like squaring numbers or finding square roots.

Algebra was first used to solve equations and inequalities. Two common types are linear equations, which make a straight line (like y=mx+b), and quadratic equations, which involve variables that are squared (like x*x).

The Story of Algebra
How Algebra Helps Solve Problems
Writing Algebra Down
Functions and Graphs
Basic Rules of Algebra
Beyond Basic Algebra
Related pages
Images for kids
See also

The Story of Algebra

Early forms of algebra were used by the Babylonians and Greek thinkers like Hero of Alexandria. But the word "algebra" comes from the Arabic word Al-Jabr. This word was in a math book called Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah.

This important book was written in the 9th century by a Persian mathematician named Muhammad ibn Mūsā al-Khwārizmī. He lived in Baghdad, Iraq, and died around 840 AD. His book was brought to Europe and translated into Latin in the 12th century. That's when it got the name 'Algebra'. Interestingly, part of Al-Khwarizmi's name also gave us the English word algorithm.

How Algebra Helps Solve Problems

Let's look at a simple algebra problem:

Sue has 12 candies, and Ann has 24 candies. They want to share so they have the same number of candies. How many candies will each have?

Here's how algebra can help solve it:

To make the candies equal, Ann needs to give some to Sue. Let x be the number of candies Ann gives to Sue.
Sue's candies plus x must be the same as Ann's candies minus x. We write this as: 12 + x = 24 - x
To solve for x, we need to get x by itself. First, subtract 12 from both sides of the equation:

12 + x - 12 = 24 - x - 12 This simplifies to: x = 12 - x

Next, add x to both sides of the equation:

x + x = 12 - x + x This gives: 2x = 12

Finally, divide both sides of the equation by 2:

2x / 2 = 12 / 2 This gives: x = 6. So, Ann gives Sue 6 candies.

To check our answer, put 6 back into the original equation where x was:

12 + 6 = 24 - 6 This gives 18 = 18, which is true! They each now have 18 candies.

With practice, algebra can help you solve problems that seem too hard otherwise. Things like building a freeway, designing a cell phone, or finding cures for diseases all use algebra.

Writing Algebra Down

In math, we have special ways to write things:

Adding z to y is written as y + z.
Subtracting z from y is written as y − z.
Dividing y by z is usually written as y/z. Sometimes you might see y ÷ z.
Multiplying y by z can be written in a few ways: y × z, y * z, y·z, or most commonly, just yz. We usually avoid "×" because it looks like the letter x. When multiplying a number by an expression, we use parentheses: y (z+1).
When we multiply a number and a letter, we put the number first: 5 × y = 5y. If the number is 1, we don't write it, because 1 times any number is that number (1 × y = y).

You don't always have to use x or y in algebra. Variables are just symbols for unknown numbers, so you can use any letter or symbol. But x and y are the most common ones.

Functions and Graphs

This graph shows the line for the equation y = 3x + 1.

A big part of algebra is studying functions. Functions are like machines: you put a number in, and you get a specific number out. When we use functions, graphs are super helpful. They give us a picture of the solutions to equations.

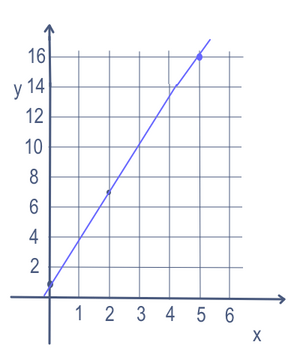
A graph shows all the values that make an equation or inequality true. It's usually easy to make a graph when there are only one or two variables. Often, the graph is a straight line. If the line isn't perfectly vertical, its basic formula is y = mx + b.

The variable b tells us where the line crosses the vertical axis (the y-axis). This is called the y-intercept.
The variable m tells us the slope or steepness of the line.

This formula works for the coordinates of a graph, where each point on the line is written as (x, y).

In equations like y = mx + b, there are two variables, x and y. To find points on the line, we change one variable, called the "independent" variable (usually x). Then we do the math to get the other number, called the "dependent" variable (usually y).

For example, in y = 3x + 1:

If we put in 5 for x, we get y = 16.
If we put in 2 for x, we get y = 7.
If we put in 0 for x, we get y = 1.

So, this line goes through the points (5,16), (2,7), and (0,1), as you can see in the graph.

If x has a power of 1 (like just x), the graph will be a straight line. If x is squared (like x²) or has another power, the graph will be curved. If the equation uses an inequality (like < or >), then part of the graph is usually shaded.

Basic Rules of Algebra

Algebra has some important rules that help us understand equations better. These rules might seem obvious, but they are very important because they don't apply in every part of mathematics. Let's look at a few:

First, two definitions:

Opposite: The opposite of a number a is $-a$ .
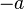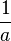Reciprocal: The reciprocal of a number a is $\frac{1}{a}$ .

Commutative Property of Addition

"Commutative" means you can swap the order of numbers without changing the result. For addition, this means: 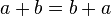$a + b = b + a$ .

Example: 3 + 5 = 8 and 5 + 3 = 8.
This rule does NOT work for subtraction! (a - b is not the same as b - a).

Commutative Property of Multiplication

For multiplication, you can also swap the order of numbers: 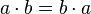$a \cdot b = b \cdot a$ .

Example: 3 × 5 = 15 and 5 × 3 = 15.
This rule does NOT work for division! (a / b is not the same as b / a, unless a and b are equal).

Associative Property of Addition

"Associative" means how you group numbers doesn't change the result. For addition, when you add three or more numbers, it doesn't matter how you group them: 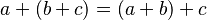$a + (b + c) = (a + b) + c$ .

Example: 2 + (3 + 4) = 2 + 7 = 9 and (2 + 3) + 4 = 5 + 4 = 9.
This rule does NOT work for subtraction.

Associative Property of Multiplication

For multiplication, when you multiply three or more numbers, it doesn't matter how you group them: 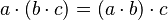$a \cdot (b \cdot c) = (a \cdot b) \cdot c$ .

Example: 2 × (3 × 4) = 2 × 12 = 24 and (2 × 3) × 4 = 6 × 4 = 24.
This rule does NOT work for division.

Distributive Property

The distributive property explains how multiplication works with addition or subtraction inside parentheses: 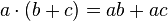$a \cdot (b + c) = ab + ac$ .

Example: 2 × (3 + 4) = 2 × 7 = 14. Using the property: (2 × 3) + (2 × 4) = 6 + 8 = 14.

Additive Identity Property

This rule states that if you add 0 to any number, the number stays the same: 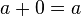$a + 0 = a$ .

Example: 7 + 0 = 7. This also works for subtraction: a - 0 = a.

Multiplicative Identity Property

This rule states that if you multiply any number by 1, the number stays the same: 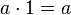$a \cdot 1 = a$ .

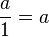Example: 7 × 1 = 7. This also works for division: $\frac{a}{1} = a$ .

Additive Inverse Property

This rule says that if you add a number and its opposite, you get 0: 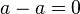$a - a = 0$ .

Example: The opposite of 5 is -5. So, 5 + (-5) = 0.

Multiplicative Inverse Property

This rule says that if you multiply a number by its reciprocal, you get 1: 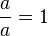$\frac{a}{a} = 1$ (as long as a is not 0).

Example: The reciprocal of 2 is 1/2. So, 2 × (1/2) = 1.

Beyond Basic Algebra

Besides "elementary algebra" (the basic algebra we've talked about), there are more advanced types of algebra taught in colleges. These include abstract algebra, linear algebra, and universal algebra.

Linear algebra helps solve many linear equations at once, often using something called a matrix.
Abstract algebra studies the general ideas found in equations, going beyond just numbers to look at groups of numbers and other mathematical structures.

Algebra is also very important in physics and engineering. In many physics problems, time is a variable, often shown as t. Other common variables are energy (e), force (f), mass (m), and acceleration (a). You might recognize famous equations like f = ma (Force equals mass times acceleration) and e=mc^2 (Einstein's energy equation). Using algebra helps simplify these complex problems.

Images for kids

The word algebra comes from the title of a book by Muhammad ibn Musa al-Khwarizmi.
Italian mathematician Girolamo Cardano published solutions to complex equations in his 1545 book Ars magna.
A Linear algebra lecture at the Aalto University.