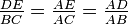Thales of Miletus facts for kids
Quick facts for kids
Thales of Miletus
|
|
|---|---|

Posthumous portrait of Thales by Wilhelm Meyer, based on a bust from the 4th century
|
|
| Born | c. 626/623 BC |
| Died | c. 548/545 BC (aged c. 78) |
| Era | Pre-Socratic philosophy |
| Region | Western philosophy |
| School | |
|
Main interests
|
|
|
Notable ideas
|
|
|
Influences
|
|
|
Influenced
|
|
Thales of Miletus (pronounced THAY-leez; born around 624/623 BC, died around 548/545 BC) was a very important thinker from ancient Greece. He lived in a city called Miletus in what is now Turkey. Thales was a mathematician, an astronomer, and a philosopher. He is often called the "Father of Science" because he was one of the first people to try to explain the world using natural ideas instead of myths.
Before Thales, people often used stories about gods to understand how the world worked. But Thales started looking for natural reasons for things. He believed that everything came from one basic substance: water. He also used geometry to solve real-world problems, like measuring the height of pyramids. Many people, including the famous philosopher Aristotle, saw him as the very first philosopher in the Greek tradition.
Contents
Life of Thales: Early Years and Journeys
We don't know the exact dates of Thales's life. But we know he was alive around 585 BC because he predicted a solar eclipse that year. Historians believe he was born in Miletus around 625 BC. He might have died around 78 years old, possibly from heatstroke while watching games.
Family Background
Some ancient writers said Thales had Phoenician ancestors, a people known for sailing and trade. But most historians agree he was from Miletus and came from a well-known Greek family. There are also different stories about his family life. Some say he married and had a son, or adopted his nephew. Others say he never married because he didn't want the worries of having children.
Did Thales Travel?
Many people believe Thales visited Egypt. It's possible because Miletus had a trading colony there. In Egypt, he might have learned about geometry. However, some historians think he could have learned about Egypt from others without actually going there. There's no strong proof he traveled to countries in the Near East.
Thales's Many Activities
Thales was known for many things. He is often called "the first Greek mathematician." He used observation, experiments, and logical thinking to understand the world.
Aristotle wrote that Thales believed water was the basic building block of everything. Thales might have thought this because all living things need moisture, and seeds are moist. He also suggested that the Earth floats on water.
Thales was also involved in engineering. Some say he didn't write any books, but others say he wrote about the sun's movements. No writings from him have survived today.
The Olive Press Story: A Smart Business Idea
There's a famous story about how Thales became rich from olives. He predicted that there would be a very good olive harvest one year. So, he rented all the olive presses in Miletus before the harvest began. When the harvest was huge, everyone needed presses, and Thales could rent them out at a high price.
Aristotle said Thales did this not to get rich, but to show people that philosophy could be useful. People often thought philosophers were just dreamers, but Thales proved they could be smart in practical ways too.
Thales as an Advisor
Thales was also a respected advisor. He once told the people of Miletus not to join forces with the Lydians in a war. Another story says he helped King Croesus's army cross a river by digging a channel to divert the water. This made the river shallower and easier to cross.
Thales's Big Ideas
Ancient civilizations often explained natural events by saying gods or heroes caused them. Thales, however, tried to explain things using natural reasons. For example, instead of saying earthquakes were caused by angry gods, he thought the Earth floated on water, and earthquakes happened when the water rocked it.
Thales also believed that everything had a kind of "soul" or life force. He thought that magnets had souls because they could move iron. He said, "all things are full of gods," meaning that a life force was present everywhere.
Geometry: Measuring the World
Thales was famous for his use of geometry. He is often seen as the first person in the Western world to use logical steps to prove geometric ideas. He understood how similar triangles work and used this knowledge in practical ways.
A story says he measured the height of the pyramids by using their shadows. He waited until his own shadow was exactly as long as he was tall. At that moment, the pyramid's shadow would also be equal to its height. This showed he understood the relationship between objects and their shadows.
He also used similar methods to measure how far ships were from the shore. This showed his practical skills in applying geometry.
Thales's Important Theorems
Two important ideas in geometry are named after Thales:
- Thales's Theorem: This states that if you draw a triangle inside a circle, and one side of the triangle is the circle's diameter, then the angle opposite the diameter will always be a right angle (90 degrees).
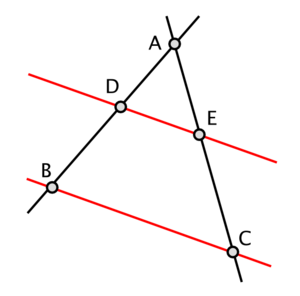
- Intercept Theorem: This theorem helps you find unknown lengths when you have parallel lines cut by two other lines.
He also discovered that a circle is divided into two equal halves by its diameter. He found that the angles at the base of an isosceles triangle (a triangle with two equal sides) are equal. And he showed that when two straight lines cross, the angles opposite each other are equal.
Water as the First Principle
Thales's most famous idea was that water was the basic substance of everything. He believed that water was the "originating principle" of nature. This means he thought everything came from water and returned to water.
Aristotle, a later philosopher, thought Thales came to this idea by seeing that all living things need moisture. He also observed that heat comes from moisture and needs it to exist. Thales also thought the Earth was a flat disk floating on a huge body of water.
Thales's Discoveries in Astronomy
Thales is famous for predicting the solar eclipse on May 28, 585 BC. This was a huge achievement for his time. He also studied the stars. He described the position of the Ursa Minor constellation, thinking it could help sailors navigate. He also calculated how long a year was and when the equinoxes (when day and night are equal) and solstices (longest/shortest days) occurred.
How Thales Influenced Others
Thales had a big impact on later Greek thinkers and Western history. Some historians believe Anaximander, another important philosopher, was his student. It's also said that Pythagoras, a very famous mathematician, visited Thales when he was young. Thales supposedly advised Pythagoras to travel to Egypt to continue his studies.
Many philosophers after Thales followed his example. They started looking for natural explanations for things instead of relying on myths. Thales helped shift thinking from "mythos" (stories about gods) to "logos" (logical reasoning and arguments). This was a major step in the development of philosophy and science.
Reliability of Information About Thales
It's important to know that much of what we know about Thales comes from stories and writings that were made hundreds of years after he lived. Because he was so famous, many legends grew around him. This makes it hard for historians to tell what is a real fact and what is just a story.
The earliest information about Thales comes from writers like Herodotus and Aristotle, who lived a few hundred years after him. Later writers, who lived much, much later, often added more stories and details. These later accounts can sometimes be less reliable.
For example, early writers saw Thales as a practical and wise man who helped his city. Later writers often made him seem like a superhuman genius who discovered everything. Historians today try to sort through these different accounts to understand the real Thales.
See also
 In Spanish: Tales de Mileto para niños
In Spanish: Tales de Mileto para niños