History of algebra facts for kids
Algebra is like doing math with puzzles! Instead of just numbers, you use letters or symbols to stand for unknown numbers. It's a way to solve problems where you don't know all the numbers yet. For a long time, algebra was mostly about solving equations.
This article will tell you about how algebra started and grew, from ancient times to when it became its own big part of mathematics.
Contents
- Where the Word "Algebra" Comes From
- How Algebra Changed Over Time
- Algebra in Ancient Babylon
- Algebra in Ancient Egypt
- Greek Geometric Algebra
- Algebra in China
- Diophantus: Early Use of Symbols
- Algebra in India
- Algebra in the Islamic World
- Algebra in Europe
- Modern Symbolic Algebra
- Who is the "Father of Algebra"?
- See also
Where the Word "Algebra" Comes From
The word "algebra" comes from the Arabic word al-jabr. This word was in the title of a famous math book written in the year 830 by a Persian mathematician named Al-Khwārizmī. His book's title, Kitāb al-muḫtaṣar fī ḥisāb al-ğabr wa-l-muqābala, means something like The Book of Completion and Balancing.
Al-jabr meant "restoration" or "completion." It was about moving numbers from one side of an equation to the other to solve it. Muqabalah meant "reduction" or "balancing," which was about canceling out similar terms on both sides. So, algebra is all about balancing equations!
How Algebra Changed Over Time
Algebra hasn't always looked the way it does today with lots of symbols. It changed a lot over many years.
Different Ways to Write Algebra
There were three main ways algebra was written:
- Rhetorical algebra: This was the earliest way. Equations were written out in full sentences. For example, to say "x + 1 = 2," they would write, "The thing plus one equals two." The ancient Babylonians used this, and it was common until the 16th century.
- Syncopated algebra: This stage started to use some symbols, but not all of them. It was a mix of words and symbols. For instance, they might use abbreviations for common words or powers. Diophantus (around 3rd century AD) and Brahmagupta (7th century) used this style.
- Symbolic algebra: This is the kind of algebra we use today, with lots of symbols for everything. Early steps were taken by Islamic mathematicians like Ibn al-Banna and Abū al-Hasan ibn Alī al-Qalasādī. But François Viète (16th century) really developed it. Later, René Descartes (17th century) introduced the modern symbols we use, like x, y, and z. He also showed how geometry problems could be solved using algebra.
Early algebra often focused on quadratic equations (equations with an x-squared term). For a long time, these equations were put into specific groups. This was because some types of quadratic equations didn't have positive answers, which was important back then.
There was also a geometric algebra used by ancient Greeks and Indians. They solved equations by drawing shapes. For example, to solve x² = A, they would find the side length of a square that had an area of A.
Big Ideas in Algebra's History
Besides how algebra was written, there were also big changes in how people thought about it:
- Geometric stage: Algebra ideas were mostly about shapes and lines. This started with the Babylonians and Greeks.
- Static equation-solving stage: The goal was to find specific numbers that fit certain rules. Al-Khwarizmi helped algebra move to this stage by creating step-by-step ways to solve problems.
- Dynamic function stage: This stage started to think about how numbers change and relate to each other, leading to the idea of a function.
- Abstract stage: This is modern algebra, where mathematicians study the rules and structures of math itself, not just specific numbers or shapes. This mostly happened in the 1800s and 1900s.
Algebra in Ancient Babylon
Algebra started with the ancient Babylonians, who lived a very long time ago (around 1900-1600 BC). They had a clever number system that helped them solve equations. They often looked for good guesses rather than exact answers.
The Babylonians were quite good at algebra. They could solve quadratic equations (equations with x-squared) and even some cubic equations (equations with x-cubed). They knew how to add the same amount to both sides of an equation or multiply both sides by the same number to simplify things. They also understood some ways to break down math problems into simpler parts.
Algebra in Ancient Egypt

Ancient Egyptian algebra was simpler than Babylonian algebra. They mostly worked with linear equations, which are equations like "x + 5 = 10."
A famous Egyptian math document is the Rhind Papyrus, written around 1650 BC. It shows problems where they solved equations like "x + ax = b." They called the unknown number "aha" or "heap." They might have used a method called "false position," where they would guess an answer, see how far off it was, and then use that to find the correct answer. Sometimes, the writer even "checked" his answers, which was an early form of showing proof!
Greek Geometric Algebra
Some people used to think the ancient Greeks didn't have algebra, but that's not quite right. The Greeks created something called geometric algebra. This meant they used lines and shapes to represent numbers and solve equations.
For example, to solve an equation like "ax = bc," the Greeks would think of it as finding a rectangle with a certain area. They would draw a rectangle with sides b and c, then extend one side to length a, and complete the shape to find the missing side, which was the answer.
Euclid of Alexandria

Euclid was a Greek mathematician who lived around 300 BC in Alexandria, Egypt. He's known as the "father of geometry" because of his book, Elements. This book is one of the most famous math textbooks ever written. It didn't have new discoveries, but it was great at explaining math ideas clearly.
Euclid's Elements showed how to solve many algebra problems using geometry. For example, he showed that a(b + c + d) = ab + ac + ad by drawing rectangles. He also showed how to solve equations like x² + ax = b² using geometric shapes.
Algebra in China
Chinese mathematics goes back a long way, at least to 300 BC.
Nine Chapters on the Mathematical Art
This book, written around 250 BC, was very important in China. It had 246 problems, including how to solve linear equations with positive and negative numbers. One problem even involved solving four equations with five unknown numbers!
Precious Mirror of the Four Elements
Written by Chu Shih-chieh in 1303, this book was a high point for Chinese algebra. The "four elements" in the title were actually four unknown numbers in his equations. The book dealt with equations that had up to 14 unknown numbers! He used a method called fan fa, which is similar to what we call Horner's method today, to solve these complex equations.
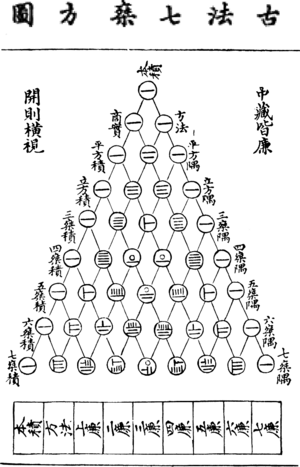
The Precious Mirror also shows a diagram of what we now call Pascal's triangle, which helps with certain math problems.
Diophantus: Early Use of Symbols
Diophantus was a Greek mathematician who lived around 250 AD. He wrote a book called Arithmetica, which was one of the first books to solve arithmetic problems using algebra. Diophantus didn't invent algebra, but he collected and used techniques that were already around.
Diophantus was one of the first to use symbols for unknown numbers and abbreviations for powers (like x-squared or x-cubed). This was a big step towards syncopated algebra. He would name an unknown, set up an equation, simplify it, and then solve it.
For example, he might write something like "x-cubed 1, x 10, minus x-squared 2, constant 1, equals constant 5." This was a way to write x³ + 10x - (2x² + 1) = 5. It was still quite wordy, but it was more symbolic than just writing full sentences.
Algebra in India
Indian mathematicians also studied number systems and algebra. They worked on linear and quadratic equations.
Brahma Sphuta Siddhanta
Brahmagupta (around 628 AD) was an Indian mathematician who wrote this book. He was important because he solved the general quadratic equation and found both positive and negative answers. He was also the first to give a general way to solve equations like ax + by = c, where a, b, and c are whole numbers. Unlike Diophantus, who often gave only one answer, Brahmagupta tried to find all the whole number answers.
Like Diophantus, Brahmagupta used a syncopated style of algebra. He put numbers side-by-side for addition, and a dot over a number for subtraction. He used abbreviations for multiplication and unknown numbers.
Bhāskara II
Bhāskara II (1114 – c. 1185) was another important Indian mathematician. He wrote books like Lilavati and Vija-Ganita, which had problems about linear and quadratic equations. He used the first letters of color names as symbols for unknown numbers! For example, if we write (-x - 1) + (2x - 8) = x - 9, he might use "ya" for the unknown and "ru" for constants, with dots for subtraction.
Algebra in the Islamic World

After a quiet period, the Islamic world had a big burst of learning in the 8th century. They translated many Greek math books into Arabic. Arabic mathematicians made algebra its own separate field of study and gave it the name "algebra."
They used a "rhetorical" style, writing out numbers and problems in words. Later, they started using Arabic numerals (like 1, 2, 3) instead of spelling out numbers. But they didn't use many symbols until much later.
Al-jabr wa'l muqabalah
The Persian mathematician Al-Khwarizmi is often called the "father of algebra." He worked in Baghdad around 850 AD. His most famous book, Al-jabr wa'l muqabalah, explained how to solve equations up to the second degree (like x-squared equations).
This book introduced the key ideas of "reduction" and "balancing." "Reduction" meant moving subtracted terms to the other side of an equation. "Balancing" meant canceling out similar terms on both sides. These are the basic steps we still use to solve equations today! The word "algebra" comes from the "al-jabr" in his book's title.
Al-Khwarizmi's book was different because it wasn't just a list of problems. It was a clear explanation of how to solve different types of equations. He used geometric drawings to prove his methods. He only worked with positive answers and recognized that some equations might not have solutions.
Other Important Islamic Mathematicians
- Abū Kāmil Shujā ibn Aslam (around 850–930) was the first to accept irrational numbers (like square roots) as answers to equations.
- Al-Karaji (953–1029) was important because he started to separate algebra from geometry. He showed how to use arithmetic operations to work with polynomials (expressions with different powers of x).
- Omar Khayyám (c. 1050 – 1123) wrote a book that went beyond Al-Khwarizmi's work, including equations of the third degree (cubic equations). He used geometric methods to solve them.
- Sharaf al-Dīn al-Tūsī (1135–1213) worked on cubic equations and even developed ideas similar to finding the maximum and minimum points of curves to solve them. He also understood the idea of a function.
- Jamshīd al-Kāshī (early 15th century) developed an early form of Newton's method to find approximate answers to equations. He also worked with decimal fractions.
- Abū al-Hasan ibn Alī al-Qalasādī (1412–1486) was one of the last major Arab algebraists. He started using letters and initial Arabic words as mathematical symbols, taking steps towards modern algebraic notation.
Algebra in Europe
After a period where not much new math was happening in Europe, the 12th century saw many Arabic math books translated into Latin. By the 13th century, European math started to catch up. The work of mathematicians like Fibonacci helped bring algebra back to life in Europe.
As the Islamic world's influence declined, Europe's influence grew, and algebra continued to develop there.
Modern Symbolic Algebra
Modern symbols for math operations (like + and -) appeared in the late 1400s and early 1500s. Then, in the late 1500s, François Viète introduced the idea of using variables (like x) to stand for unknown numbers. This was a huge step! It meant people could work with algebraic expressions as if they were numbers, making algebra much more powerful.
Another big step was finding ways to solve cubic and quartic equations (equations with x-cubed and x-to-the-fourth) in the mid-1500s. Later, in the 1600s, mathematicians like Kowa Seki and Gottfried Leibniz developed the idea of a determinant and matrices to solve systems of equations.
The Symbol x
Today, we usually use x for the first unknown number in an algebra problem, then y and z for others. This x is usually written in italic letters so it doesn't look like a multiplication sign.
Most math historians agree that René Descartes (in 1637) was the one who started using x, y, and z for unknowns. He used letters from the beginning of the alphabet (a, b, c) for numbers he already knew, and letters from the end (z, y, x) for the unknowns. Some say he chose x because it was a common letter in printing presses at the time.
There's a popular story that x came from an Arabic word for "thing" (shay) that was written as xei in Old Spanish. But historians have found that early Spanish mathematicians used the Spanish word "cosa" (meaning "thing") instead, so the x likely came from Descartes.
Gottfried Leibniz
Gottfried Leibniz (late 1600s) was the first to clearly use the idea of a function. He saw that numbers in a system of linear equations could be put into a grid, called a matrix, which could then be used to find the solution. This method is now called Gaussian elimination. Leibniz also discovered Boolean algebra, which is important in computer science.
Abstract Algebra
Over time, algebra became less about specific numbers and more about the general rules and structures of math. This led to abstract algebra, which studies things like polynomials, complex numbers, and other mathematical ideas in a very general way. It's a big part of modern mathematics.
Who is the "Father of Algebra"?
The title "father of algebra" is often given to the Persian mathematician Al-Khwarizmi. Many math historians support this. However, some people argue that the Greek mathematician Diophantus deserves the title.
Those who support Diophantus point out that his algebra in Arithmetica used more symbols (syncopated) than Al-Khwarizmi's Al-Jabr, which was mostly written in words (rhetorical). But some historians say Diophantus's math wasn't much more advanced than the ancient Babylonians.
Those who support Al-Khwarizmi say he gave a complete explanation for solving quadratic equations and was the first to teach algebra as its own subject. He also introduced the key ideas of "reduction" and "balancing" (al-jabr). His book was a systematic guide to solving equations, not just a collection of problems. Many see Al-Jabr as the first true algebra textbook we still have today.
Before modern times, algebra was often used by merchants and surveyors. Diophantus used it for specific problems, while Al-Khwarizmi wrote one of the first general books on how to solve equations.
See also
- Timeline of algebra





