Apollonius of Perga facts for kids
Apollonius of Perga (Greek: Ἀπολλώνιος ὁ Περγαῖος, translit. Apollṓnios ho Pergaîos; Latin: Apollonius Pergaeus; c. 240 BCE/BC – c. 190 BCE/BC) was an Ancient Greek geometer and astronomer. He is famous for his important work on conic sections. These are shapes like ellipses, parabolas, and hyperbolas. His definitions for these shapes are still used today.
Apollonius also worked on many other topics, including astronomy. Most of his writings on these subjects are now lost. He suggested that planets move in "eccentric orbits." This idea was popular for a long time, until the Renaissance. A crater on the Moon is named after him.
Life of Apollonius
We don't know much about Apollonius's life, even though he was a very important mathematician.
He was born in Perga, a Greek city in Anatolia. The city's ruins can still be seen today. It was a place where Greek culture was strong. Apollonius lived around the time of Ptolemy III Euergetes, who was a Greek ruler of Egypt from 246 to 221 BC. We don't know his exact birth or death dates.
Apollonius likely lived, studied, and wrote in Alexandria, Egypt. This city was a major center for learning in the ancient world. He probably studied with the students of Euclid, another famous Greek mathematician.
His Famous Book: Conics
Apollonius wrote a major work called Conics. It had eight books. He sent parts of it to his friends, like Eudemus, asking them to review his work. This shows he was a young mathematician looking for advice from older experts. Later, he sent books to a person named Attalus. This Attalus might have been Attalus II Philadelphus, a king who loved collecting books.
Apollonius planned to write eight books for Conics. Only the first four books are still mostly complete in their original Greek form. Books 5-7 only exist because they were translated into Arabic. The eighth book is lost, and we don't know if he ever finished it.
Apollonius's Works
Apollonius wrote many books, but only Conics has survived. Even then, parts of it are only available in Arabic translations.
About Conics
Conics is a very detailed book. It has 387 mathematical statements (called propositions) in its first seven books. It's set up like a modern geometry textbook, with definitions and proofs.
Scholars have studied Conics for centuries. Many have tried to explain Apollonius's ideas in simpler ways or using modern math symbols.
Book I: The Basic Shapes
Book I has 58 propositions. It gives the main definitions of cones and conic sections.
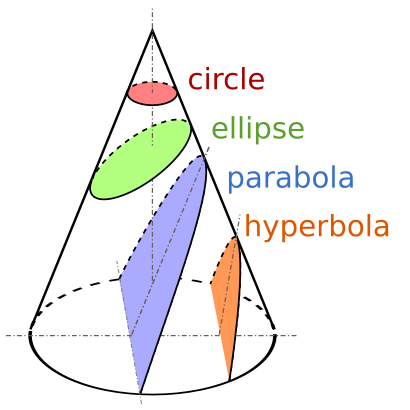
- A cone is a 3D shape with a point (called the vertex) and a circular base.
- A "section" is what you get when you cut a cone with a flat surface (a plane).
- If you cut a cone through its vertex, you get a triangle.
- If you cut a cone parallel to its base, you get a circle.
- Apollonius defined the ellipse, parabola, and hyperbola:
- An ellipse is made by cutting a single cone at an angle.
- A parabola is made by cutting a single cone parallel to one of its sides.
- A hyperbola is made by cutting a double cone (two cones joined at their vertices) parallel to its central line. This cut creates two separate curves.
Apollonius used a method called "application of areas." This was a way to describe geometric relationships that are like equations in modern algebra. For example, he showed how the area of a square built on one part of a parabola relates to a rectangle built on another part. This led to the names of the shapes:
- Parabola means "application" or "exact fit."
- Ellipse means "deficit" or "falling short."
- Hyperbola means "excess" or "overshooting."
Book II: Key Features
Book II has 53 propositions. It talks about important features of conic sections, like their "diameters" and "axes." It also covers "asymptotes" (lines that a curve gets closer and closer to but never touches) and "tangents" (lines that touch a curve at only one point).
Book III: New Discoveries
Book III has 56 propositions. Apollonius said he discovered new theorems here. These theorems helped solve problems about "loci," which are sets of points that follow a certain rule. For example, he described the "three-line locus" and "four-line locus" problems, which are ways to find points that form conic sections.
Book IV: How Shapes Meet
Book IV has 57 propositions. It explores how many times conic sections can cross each other, or how many times they can cross a circle.
Book V: Shortest and Longest Lines
Book V has 77 propositions. It focuses on finding the shortest and longest lines that can be drawn from a point to a conic section. This book is complex, and scholars still debate its exact meaning. Some think it's about lines that are perpendicular to the curve (called "normals").
Book VI: Similar Shapes
Book VI has 33 propositions. It discusses "equal and similar sections of cones." Apollonius extended the ideas of congruence (being exactly the same shape and size) and similarity (being the same shape but different sizes) to conic sections.
Book VII: Diameters and Conjugates
Book VII has 51 propositions. It goes into detail about "diameters" and "conjugate diameters" of conic sections. A diameter is a line that cuts a curve in half. For shapes like circles and ellipses, conjugate diameters are pairs of diameters that are related in a special way, showing the shape's symmetry.
Lost Works Mentioned by Others
Pappus of Alexandria, another ancient mathematician, wrote about other books by Apollonius that are now lost. These include:
- De Rationis Sectione ("Cutting of a Ratio"): About finding a line that cuts two other lines in a specific ratio.
- De Spatii Sectione ("Cutting of an Area"): Similar to the above, but about areas.
- De Sectione Determinata ("Determinate Section"): About finding points on a line based on their distances from other points.
- De Tactionibus ("Tangencies"): About drawing a circle that touches other points, lines, or circles. This is sometimes called the "Problem of Apollonius."
- De Inclinationibus ("Inclinations"): About placing a line of a certain length between two other lines.
- De Locis Planis ("Plane Loci"): A collection of ideas about points that form straight lines or circles.
Other ancient writers also mentioned lost works by Apollonius, such as:
- On the Burning-Glass: Likely about how parabolas can focus light.
- On the Cylindrical Helix: About a spiral shape on a cylinder.
- A comparison of a 12-sided shape (dodecahedron) and a 20-sided shape (icosahedron) inside the same sphere.
- A general work on mathematics, possibly with his ideas for improving Euclid's Elements.
- Quick Bringing-to-birth: Where he found better ways to estimate the value of π than Archimedes.
- A book on how to write and multiply very large numbers.
Apollonius's Ideas
Astronomy Contributions
Apollonius is credited with showing that two different ways of describing how planets move are actually the same. One way uses "excentrics" (off-center circles), and the other uses "deferent and epicycles" (circles moving on other circles). This idea was important in astronomy for a long time.
Apollonius's Math Methods
Apollonius and other Greek geometers used a way of thinking about math that is sometimes called "geometrical algebra." They didn't use symbols like 'x' or 'y' for numbers as we do today. Instead, they used lines and areas to represent numbers and solve problems.
For example, to find the area of a square, they would literally draw a square. When we write a2 + b2 = c2 for the Pythagorean theorem, they would say "the square on line a plus the square on line b equals the square on line c."
Apollonius's Coordinate System
Apollonius used a kind of coordinate system in his work. He would place his shapes in a specific way, using a "diameter" as a horizontal line (like our x-axis) and the "vertex" (a point on the curve) as an origin. Distances from the curve to the diameter were called "ordinates" (like our y-coordinates).
While not exactly like our modern Cartesian coordinate system (which uses negative numbers and covers all space), Apollonius's system was an important step towards it.
The Theory of Proportions
Apollonius used the "Theory of Proportions" from Euclid's Elements. This theory helps compare sizes or "magnitudes" of things.
- A "magnitude" is any size that can be divided into units.
- A "ratio" (Greek: logos) is a way to compare two magnitudes. For example, the ratio of line AB to line CD tells you how many times CD fits into AB. This is like our modern fractions.
- A "proportion" (Greek: analogos) states that two ratios are equal. For example, if line AB is to line CD as line EF is to line GH. This is like saying AB/CD = EF/GH in algebra.
Apollonius used these ideas to describe the relationships within conic sections, often comparing areas of squares and rectangles.
Images for kids
-
The animation shows how Apollonius used "application of areas" to describe a parabola. The orange square and blue rectangle relate to points on the curve. In algebra, this is like the equation x² = py.
-
A modern Cartesian coordinate system, which uses x and y axes to locate points. Apollonius used a similar, but simpler, system.
-
The Pythagorean theorem shown visually. The area of the blue square equals the sum of the areas of the other two squares.
-
Pages from a 9th-century Arabic translation of Apollonius's Conics.
-
A 1654 printed edition of Apollonius's Conica.
See also
In Spanish: Apolonio de Perge para niños
- Apollonian circles
- Apollonian gasket
- Apollonius point
- Apollonian network
- Apollonius' theorem
- Circles of Apollonius
- Descartes' theorem
- Problem of Apollonius
