Aristarchus of Samos facts for kids
Quick facts for kids
Aristarchus of Samos
|
|
|---|---|

Statue of Aristarchus of Samos at the Aristotle University of Thessaloniki
|
|
| Born | c. 310 BCE |
| Died | c. 230 BCE (age c. 80) |
| Nationality | Greek |
| Occupation | |
Aristarchus of Samos (born around 310 BCE, died around 230 BCE) was an amazing ancient Greek astronomer and mathematician. He was the first person we know of to suggest a heliocentric model of the universe. This means he believed the Sun was at the center, and the Earth moved around it once a year, while also spinning on its own axis once a day.
Aristarchus was a student of Strato of Lampsacus. Strato was a leader at the Peripatetic School in Greece. During his time there, Aristarchus observed the summer solstice in 280 BCE. Besides his ideas about the Sun being the center, he also invented two types of sundials. One was a flat disc, and the other was shaped like a half-sphere.
Aristarchus was inspired by an idea from Philolaus. Philolaus thought there was a "central fire" in the universe. Aristarchus agreed, but he said this "central fire" was actually the Sun. He then correctly placed the other planets in their order around the Sun.
Like Anaxagoras before him, Aristarchus thought that stars were just like our Sun, but much, much farther away. However, his ideas were often not accepted. Most people at the time believed in geocentric theories. These theories, supported by thinkers like Aristotle and Ptolemy, said that the Earth was the center of the universe. Later, Nicolaus Copernicus knew that Aristarchus had a theory about a "moving Earth." But it's not clear if Copernicus knew it was a full heliocentric theory.
Aristarchus also estimated the sizes of the Sun and Moon compared to Earth. He also figured out how far away the Sun and Moon were from Earth. He is seen as one of the greatest astronomers from ancient times, along with Hipparchus. He is also considered one of the most important thinkers in human history.
The Sun at the Center
Aristarchus believed the stars were other suns, very far away. Because they were so far, he thought there would be no noticeable parallax. Parallax is the apparent shift in the position of stars as the Earth moves around the Sun. At that time, people couldn't prove this idea because they didn't have telescopes. Stellar parallax can only be seen with telescopes.
Some people mistakenly think that Aristarchus's heliocentric idea was seen as disrespectful to the gods by his friends. But this isn't true. A writer named Plutarch wrote about Aristarchus joking with Cleanthes. Cleanthes was a leader of the Stoics and worshipped the Sun. He was against the idea of the Sun being the center. In Plutarch's original writing, Aristarchus joked that Cleanthes should be charged with disrespect. But later, someone changed the text, making it seem like Aristarchus was the one being called disrespectful. This led to the wrong idea that Aristarchus was alone and treated badly for his ideas.
According to Plutarch, Aristarchus only suggested heliocentrism as a possible idea. But a century later, Seleucus of Seleucia, another astronomer, believed it was definitely true. He even tried to prove it, but we don't have his full proof today. Later, Pliny the Elder wondered if mistakes in predicting the heavens were because the Earth wasn't at the center. Pliny and Seneca also talked about the retrograde motion of some planets. They said this backward movement was only an appearance, not real. This idea fits with heliocentrism, not geocentrism.
However, since no stellar parallax was observed, thinkers like Plato, Aristotle, and Ptolemy preferred the geocentric model. This model, which put Earth at the center, was believed to be true throughout the Middle Ages.
The idea of the Sun being the center was brought back by Copernicus. After him, Johannes Kepler described how planets move even more accurately with his three laws. Later, Isaac Newton explained why planets move this way using his laws of gravity.
Aristarchus realized that the Sun was much bigger than the Earth and other planets. This led him to conclude that the planets must be orbiting the Sun.
How Far is the Sun?
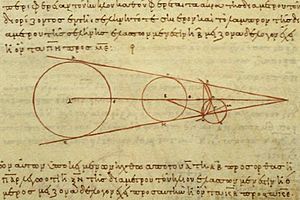
Aristarchus wrote a book called On the Sizes and Distances of the Sun and Moon. In this book, he tried to figure out the sizes and distances of these celestial bodies.
He used a clever method. He claimed that when the Moon was exactly half full, the angle between the Sun and the Moon, as seen from Earth, was 87 degrees. This angle is very hard to measure perfectly without tools.
Using correct geometry but his 87-degree measurement, Aristarchus figured out that the Sun was about 18 to 20 times farther away from Earth than the Moon. (The actual angle is closer to 89.5 degrees, and the Sun is about 400 times farther away than the Moon.) Even with his slightly off measurement, his method was brilliant for his time. He also noticed that the Moon and Sun appear to be almost the same size in the sky. This meant their actual sizes must be related to their distances from Earth.
Size of the Moon and Sun
In his book, Aristarchus also talked about the sizes of the Moon and Sun compared to Earth. To do this, he watched a lunar eclipse. He noted how long it took for Earth's shadow to cover the Moon and how long the Moon stayed in the shadow.
From this, he estimated the size of Earth's shadow. He figured out that the shadow was twice the diameter of the Moon. He also estimated that the shadow extended about 2.4 times the distance of the Moon from Earth.
Using these calculations and his estimated distances, he used geometry to find the Moon's size. He determined that the Moon's diameter is about one-third the size of Earth's diameter.
To estimate the Sun's size, Aristarchus used the idea that the Sun's distance from Earth was about 18 to 20 times the Moon's distance. Since the Sun and Moon look about the same size in the sky, he concluded that the Sun must be about 19 times wider than the Moon. This would make the Sun roughly six times wider than Earth.
Legacy
The lunar crater Aristarchus is named after him. So is the minor planet 3999 Aristarchus. Also, the Aristarchos telescope is named in his honor.
See also
 In Spanish: Aristarco de Samos para niños
In Spanish: Aristarco de Samos para niños
- Aristarchus's inequality
- Eratosthenes (born around 276 BCE), a Greek mathematician who calculated the circumference of the Earth and also the distance from the Earth to the Sun.
- Hipparchus (born around 190 BCE), a Greek mathematician who measured the radii of the Sun and the Moon as well as their distances from the Earth.
- Posidonius (born around 135 BCE), a Greek astronomer and mathematician who calculated the circumference of the Earth.