Patterns in nature facts for kids

Kids Encyclopedia Facts

Patterns in nature are amazing shapes and designs you can see all around you in the natural world. These patterns show up again and again in different places, and sometimes we can even explain them using math! Think about the perfect shapes of snowflakes, the spirals in a sunflower, or the stripes on a zebra.

Scientists have been curious about these patterns for a long time. Ancient Greek thinkers like Plato and Pythagoras tried to understand why nature has so much order. Later, in the 1800s, people like Joseph Plateau studied soap films, and Ernst Haeckel drew hundreds of sea creatures to show off their amazing symmetry. D'Arcy Thompson looked at how plants and animals grow, finding that simple math could explain spiral shapes. In the 1900s, Alan Turing, famous for his work with computers, even predicted how patterns like spots and stripes could form in living things. Other scientists like Benoît Mandelbrot showed how "fractals" – complex, repeating patterns – could describe how plants grow.

Math, physics, and chemistry help us understand these patterns. For living things, patterns are also shaped by biology, especially by how creatures change over time to survive and reproduce (this is called natural selection and sexual selection). Scientists often use computer models to create and study these patterns.

History of Studying Patterns
Why Patterns Form
Types of Patterns
How Patterns Form
Images for kids
See also

History of Studying Patterns

You can find Fibonacci patterns in many plants, like the cone of this queen sago plant.

People have been trying to understand patterns in nature for thousands of years.

Ancient Greeks: Philosophers like Plato thought that physical objects were just imperfect copies of perfect, ideal shapes. So, a flower might look like a circle, but it's never a perfect mathematical circle. Pythagoras believed that numbers were the key to understanding everything, including the patterns in nature and even music.
Middle Ages: Around 1202, an Italian mathematician named Leonardo Fibonacci introduced a special number sequence (1, 1, 2, 3, 5, 8...) to the Western world. He used a made-up example of rabbits growing to show how these numbers appear in nature.
1600s: Sir Thomas Browne, an English thinker, wrote about how "Nature Geometrizeth" (meaning nature uses geometry). He pointed out the five-point "quincunx" pattern in plants.
Early 1900s: D'Arcy Wentworth Thompson wrote a famous book in 1917 called On Growth and Form. He showed how the Fibonacci sequence and other math ideas explain the spiral growth patterns in plants, animal horns, and even seashells.
1800s: The Belgian physicist Joseph Plateau studied soap films and found that they naturally form shapes with the smallest possible surface area. He came up with rules, now called Plateau's laws, that describe how bubbles and foams are structured.
Late 1800s: German biologist Ernst Haeckel created beautiful drawings of sea creatures, highlighting their amazing symmetry.
Mid-1900s: In 1952, Alan Turing, a brilliant British mathematician, wrote about how patterns like spots and stripes could form in living things through a process called morphogenesis. He suggested that chemicals reacting and spreading (diffusing) could create these patterns.
Late 1900s: In 1968, Aristid Lindenmayer developed "L-systems," which are like mathematical rules that can create realistic models of how plants grow, often looking like fractals. In 1975, Benoît Mandelbrot brought together many mathematical ideas into the concept of the fractal, which describes shapes that look similar at different scales.

Why Patterns Form

These aphids are clustered on a sycamore leaf. The leaf's veins create patterns that the young aphids avoid.

When you look at beautiful things in nature, like colorful orchids or a peacock's tail, you might wonder why they look the way they do. The beauty comes from different reasons:

Mathematics: Math helps us find and explain abstract patterns. Things like chaos theory, fractals, and spirals are all mathematical ideas that help explain visual patterns in nature. For example, L-systems can create very realistic models of how trees grow.
Physics: The rules of physics apply mathematical ideas to the real world. For instance, the way rivers bend (called meanders) can be explained by how fluids move.
Biology: In living things, natural selection plays a big role. Patterns can develop to help animals hide (camouflage), attract mates (sexual selection), or send signals. For example, the shapes and colors of flowers have evolved to attract insects like bees, helping the plants reproduce. Some patterns, visible only in ultraviolet light, act as "nectar guides" to show insects where to find food.

Types of Patterns

Symmetry

Symmetry means that a shape looks the same when you flip it, turn it, or move it.

Mirror Symmetry: Many animals, like tigers, and plant leaves have mirror symmetry. This means if you draw a line down the middle, one side is a perfect reflection of the other.
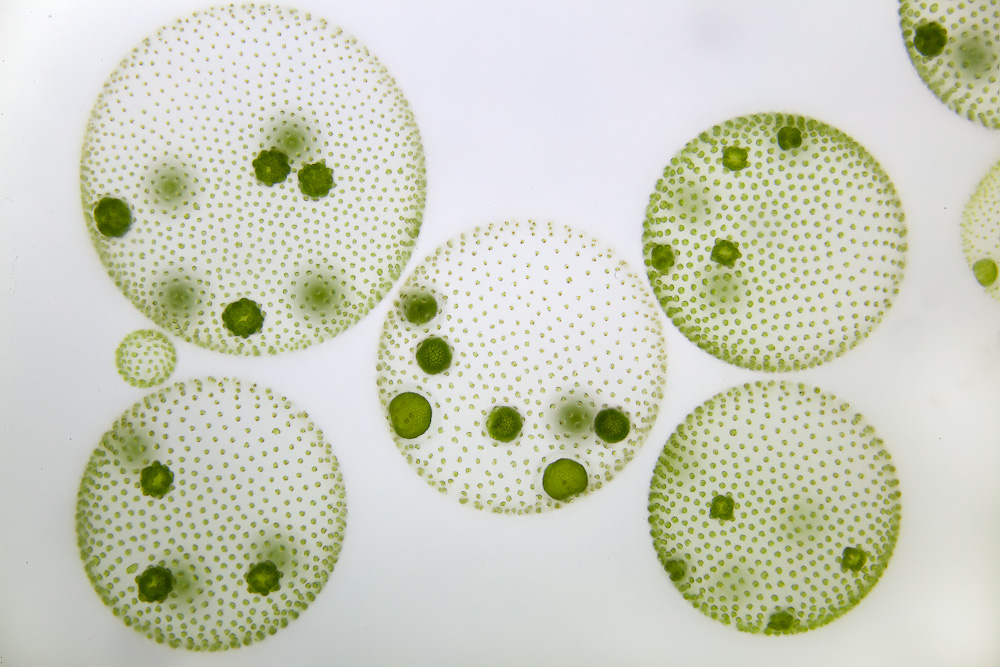
Radial Symmetry: Plants often have radial symmetry, like many flowers and sea anemones. This means they look the same if you rotate them around a central point.
Fivefold Symmetry: You can see fivefold symmetry in starfish and sea urchins. They have five parts arranged around a center.
Sixfold Symmetry: Snowflakes are famous for their beautiful sixfold symmetry. Each arm of a snowflake grows in a similar way, creating a repeating pattern.
Crystals: Crystals also show many types of symmetry, like cubic shapes.

Why do living things have symmetry? Animals that move in one direction, like humans, usually have mirror symmetry because they need a front, back, top, and bottom. Animals that stay in one place, like sea anemones, often have radial symmetry because food or danger can come from any direction.

Trees and Fractals

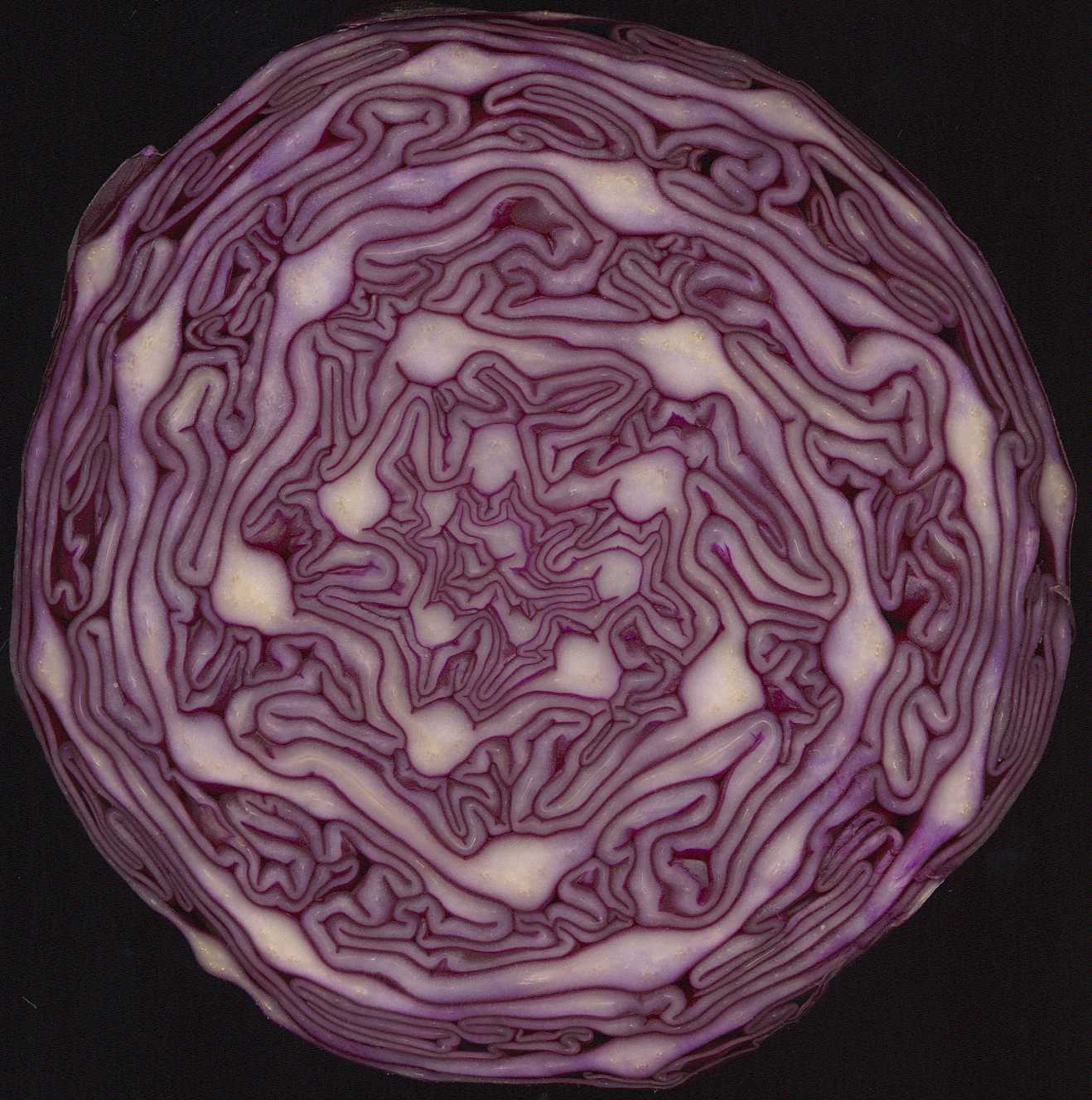
Fractals are special patterns that look similar no matter how much you zoom in or out. Think of a fern leaf: each small part of the leaf looks like a tiny version of the whole leaf. In nature, patterns aren't perfectly fractal because things don't repeat infinitely, but they can be very close.

You can see fractal-like patterns everywhere:

In the branching of trees and plants.
In the shapes of clouds and river networks.
In coastlines and mountains.
In the patterns on animal fur.
In snowflakes and crystals.

Scientists use "L-systems" (Lindenmayer systems) to create computer models of how trees grow, changing small details like branching angles to get different tree shapes.

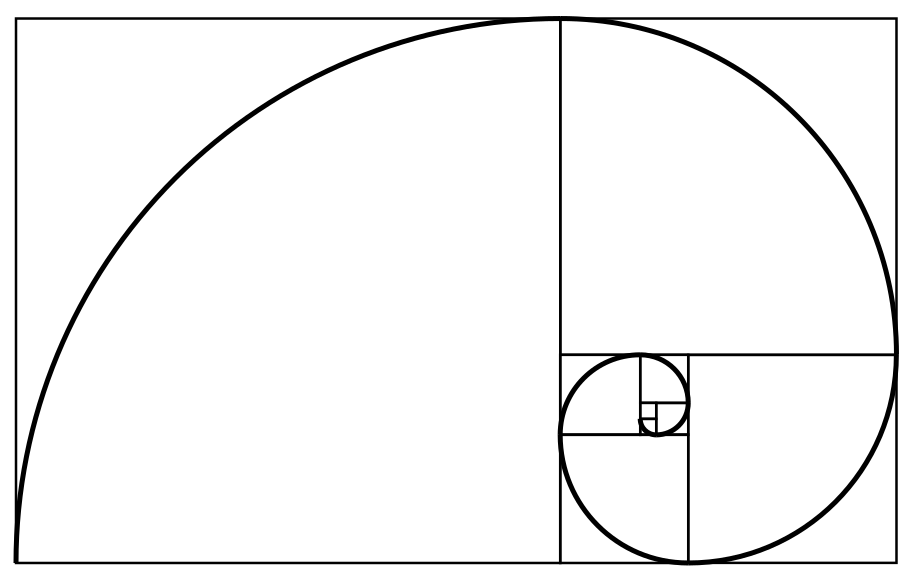
Spirals

Spirals are very common in plants and some animals, especially snails and shells. For example, in a nautilus shell, each new chamber is a slightly larger copy of the last one, forming a beautiful logarithmic spiral.

You can see plant spirals in:

The way leaves are arranged on a stem (called phyllotaxis).
The patterns of seeds in a sunflower head.
The scales on a pineapple or a pine cone.

These plant spirals often follow the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13...). For example, if you count the spirals in a sunflower head, you'll often find two sets of spirals going in opposite directions, and the number of spirals in each set will be Fibonacci numbers, like 34 and 55.

Why do spirals form?

Physics: Spirals are often the most energy-efficient shapes that form naturally.
Chemistry: They can be created by chemical reactions where certain substances activate or stop growth in a spiral pattern.
Biology: For plants, arranging leaves in a spiral helps them get the most sunlight for photosynthesis.

Chaos, Flow, and Meanders

Chaos: In math, a chaotic system is one where a tiny change at the beginning can lead to very different results later on. This is sometimes called the "butterfly effect". Even though it sounds random, chaotic systems can still create patterns.
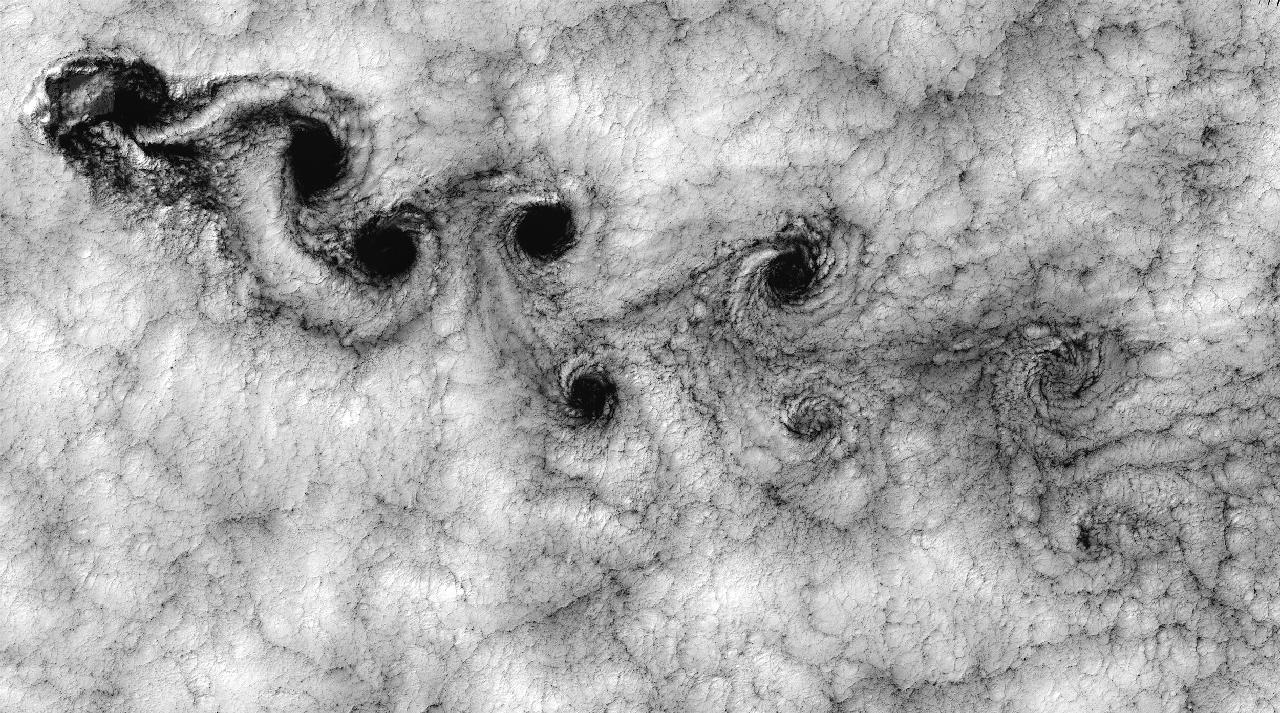
Vortex Streets: When fluid (like air or water) flows around an object, it can create zigzagging patterns of swirling shapes called vortex streets. You can see these in clouds or behind a boat in water.
Meanders: Rivers often don't flow in a straight line; they form winding bends called meanders. This happens because the water flows faster on the outside of a bend, causing more erosion there, and slower on the inside, where sand builds up. This process makes the bends grow bigger and bigger over time.

Waves and Dunes

Waves: Waves are disturbances that carry energy. In water or air, they make the medium move up and down as they pass. Wind blowing over water creates the familiar patterns of ocean waves.
Ripples and Dunes: When wind or water waves move over sand, they create patterns of ripples. When strong winds blow over large areas of sand, they form bigger shapes called dunes. Dunes can have many different patterns, like crescents, long straight lines, or star shapes.
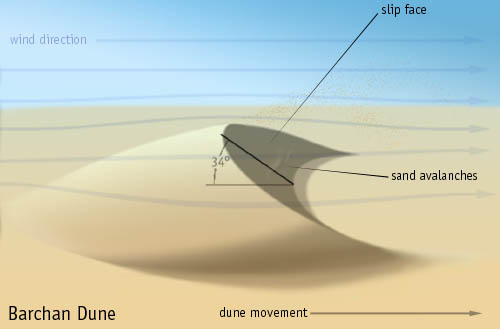
Barchan Dunes: These are crescent-shaped dunes formed by wind in deserts. The wind pushes sand up one side, and it falls down the other side, creating a steep "slip face." This process makes the dune move slowly across the desert.

Bubbles and Foam

Soap Bubbles: A single soap bubble always forms a perfect sphere. This is because a sphere has the smallest possible surface area for the amount of air it holds.
Foam: A foam is a collection of many bubbles. In foams, three soap films usually meet at each edge at a 120-degree angle, and four edges meet at each corner at about 109.5 degrees. These are called Plateau's laws.
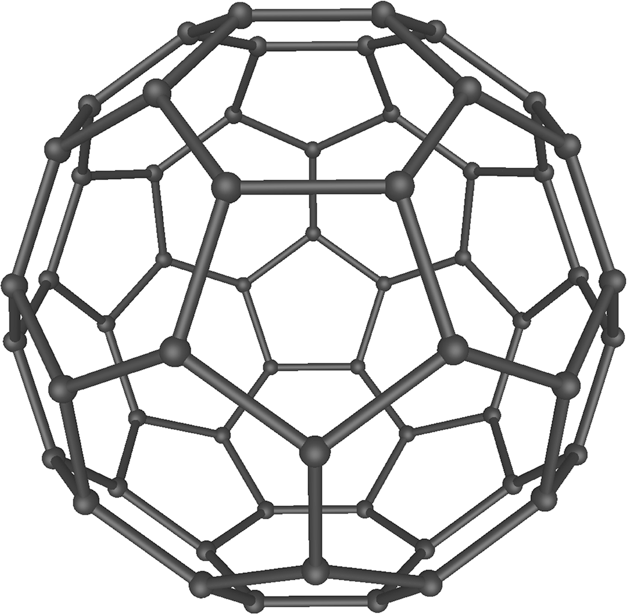
Natural Foams: You can see foam-like patterns in the tiny skeletons of some sea creatures, like Radiolaria, and even in the structure of a sea urchin's skeleton. Interestingly, a sphere made only of hexagons is impossible; any closed shape made of hexagons must also include exactly 12 pentagons, just like a soccer ball!

Tessellations

Tessellations are patterns made by repeating tiles that fit together perfectly without any gaps. While artists often use tessellations, they are also found in nature:

Honeycomb: Honey bees build their honeycombs with perfect hexagonal cells, which is a great example of a natural tessellation.
Scales: The scales on fish, reptiles, or fruits like the snake fruit often form repeating, overlapping patterns.
Crystals: The atoms in minerals form very regular, repeating three-dimensional arrangements, which are like tessellations in 3D.

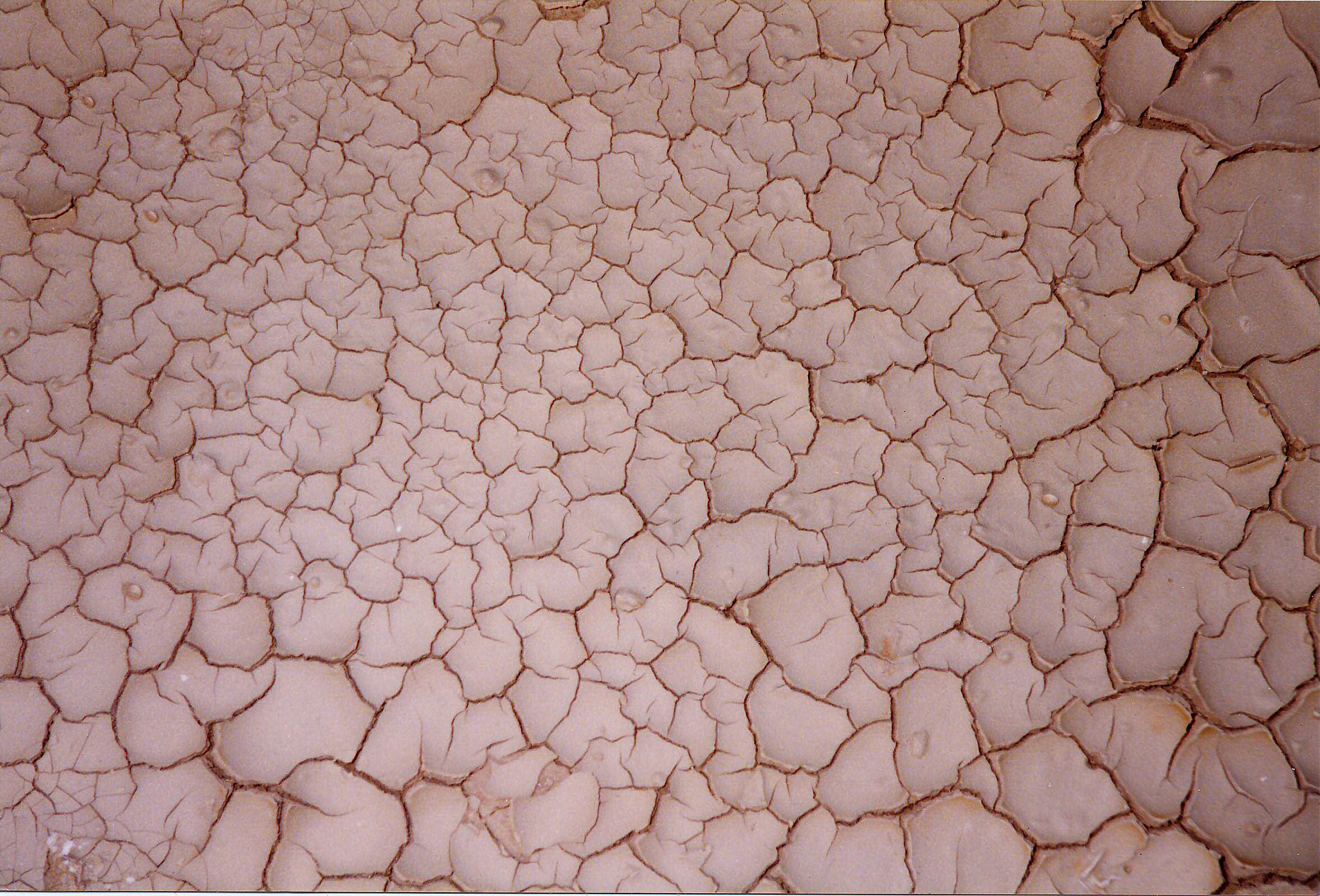
Cracks

Cracks are lines that form in materials when they are under stress. The way cracks form can tell us about the material:

Elastic Materials: If a material can stretch or shrink a lot before breaking (like elastic mud), the cracks will often meet at 120-degree angles. Think of the hexagonal columns at the Giant's Causeway.
Inelastic Materials: If a material is stiff and doesn't stretch much (like dry mud or old pottery glaze), the cracks will often form at 90-degree angles.
Tree Bark: The bark of a tree cracks to relieve stress as the tree grows. Because each tree species has a different internal structure, each has its own unique pattern of cracks in its bark.

Spots and Stripes

Animals like leopards have spots, and zebras have stripes. These patterns aren't just for show; they have important jobs that help the animals survive and have babies.

Camouflage: Patterns can help animals blend in with their surroundings, making it harder for predators to see them. A leopard's spots help it hide in the dappled light of the jungle, making it a better hunter.
Signaling: Some patterns are meant to be seen! A ladybird's bright colors and spots warn birds that it tastes bad or is poisonous. A young bird might try to eat a ladybird once, but it will quickly learn to avoid them. This helps the ladybirds survive.

So, while these reasons explain *why* animals need these patterns, they don't explain *how* the patterns actually form on their bodies.

How Patterns Form

Scientists like Alan Turing and James Murray have described a way that spots and stripes can form on their own, called a reaction-diffusion system.

Imagine a young animal's skin cells. They have genes that can be turned on by a chemical signal, called a morphogen. If this morphogen is spread evenly, the animal might be all one color. But if it's unevenly spread, spots or stripes can appear.

Turing suggested that the morphogen itself could control its own production. Also, there might be a second chemical, an inhibitor, that stops the morphogen from being made. If this inhibitor spreads faster than the morphogen, it can create areas where the morphogen is strong (making a spot or stripe) and areas where it's weak. The Belousov–Zhabotinsky reaction is a real-life chemical example of this kind of system, where chemicals change color in a repeating pattern.

Scientists have used these ideas to create computer models that look just like zebra stripes, jaguar spots, and ladybird patterns. More complex models can even show how patterns on a single feather can change from stripes at the bottom to dots at the tip.

Patterns can also form in landscapes:

Tiger Bush: In dry areas, plants grow in stripes on slopes. Each stripe of plants collects rainwater for the plants below it, creating a repeating pattern.
Fir Waves: In mountain forests, when trees fall, they expose the trees behind them to wind damage. This creates gaps that expand downwind. Meanwhile, new young trees grow in the sheltered areas, leading to waves of trees.
Patterned Ground: In very cold places where the ground freezes and thaws every year, the soil can form patterns like circles, nets, or polygons. This happens as water freezes in cracks, expanding and widening them.
Fairy Circles: In Namibia, mysterious bare circles in the grass are thought to be created by termites or by plants competing for water.
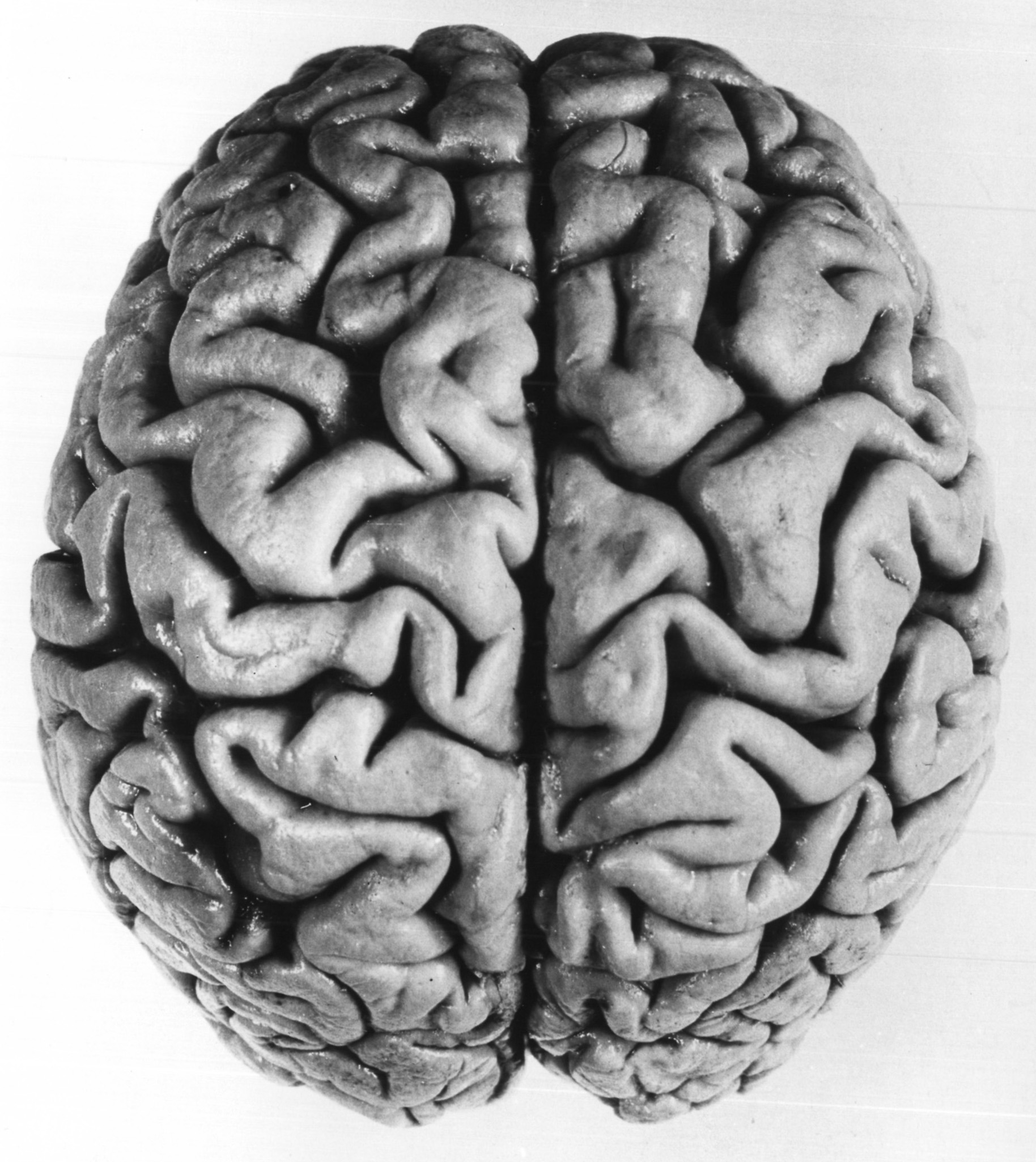
Brain Patterns: Even the wrinkled surface of our brains, with its ridges and grooves, forms a pattern. This is caused by the way the outer layer of the brain expands during development, creating folds to fit into the skull.

Images for kids

Beijing's National Aquatics Center for the 2008 Olympic games has a Weaire–Phelan structure.
Branching pattern of a baobab tree.
The leaf of cow parsley is divided into many smaller parts.
Fractal spirals: Romanesco broccoli shows a self-similar form.
Angelica flowerhead, a sphere made of spheres (self-similar).
Flow: Vortex street of clouds at Juan Fernandez Islands.
Crystals: Cube-shaped crystals of halite (rock salt).
Arrays: Honeycomb is a natural tessellation.
A group of ladybirds by G.G. Jacobson.