Pierre-Simon Laplace facts for kids

Kids Encyclopedia Facts

Quick facts for kids Pierre-Simon Laplace
Pierre-Simon Laplace as chancellor of the Senate under the First French Empire
Born	(1749-03-23)23 March 1749 Beaumont-en-Auge, Normandy, Kingdom of France
Died	5 March 1827(1827-03-05) (aged 77) Paris, Kingdom of France
Nationality	French
Alma mater	University of Caen
Known for	Work in celestial mechanics Predicting the existence of black holes Bayesian inference Bayesian probability Laplace's equation Laplacian Laplace transform Inverse Laplace transform Laplace distribution Laplace's demon Young–Laplace equation Laplace number Laplace limit Laplace invariant Laplace principle Laplace's principle of insufficient reason Laplace's method Laplace force Laplace filter Laplace functional Laplacian matrix Laplace motion Laplace plane Laplace pressure Laplace resonance Laplace's spherical harmonics Laplace smoothing Laplace expansion Laplace expansion Laplace-Bayes estimator Laplace–Stieltjes transform Laplace–Runge–Lenz vector Nebular hypothesis
Scientific career
Fields	Astronomy and Mathematics
Institutions	École Militaire (1769–1776)
Academic advisors	Jean d'Alembert Christophe Gadbled Pierre Le Canu
Notable students	Siméon Denis Poisson Napoleon Bonaparte



Minister of the Interior
In office 12 November 1799 – 25 December 1799
Prime Minister	Napoleon Bonaparte (as First Consul)
Preceded by	Nicolas Marie Quinette
Succeeded by	Lucien Bonaparte



Signature

Pierre-Simon Laplace (born March 23, 1749 – died March 5, 1827) was a brilliant French scientist. He was a master of many subjects, including engineering, mathematics, statistics, physics, astronomy, and philosophy. People sometimes called him the "French Newton" because his work was so important.

Laplace brought together and expanded on the ideas of scientists who came before him. His most famous work, Celestial Mechanics, was a five-volume book published between 1799 and 1825. In this book, he used calculus to study how planets move, which helped solve many complex problems. He also played a big role in developing Bayesian probability, a way of understanding how likely events are.

He created Laplace's equation and the Laplace transform, which are used a lot in mathematical physics. The Laplace operator, another important math tool, is also named after him. Laplace also helped develop the idea that our Solar System formed from a spinning cloud of gas and dust. He was even one of the first scientists to imagine something like a black hole.

Laplace was considered one of the greatest scientists ever. He was so good at math that he was even Napoleon Bonaparte's examiner when Napoleon attended military school in 1784. Later, Laplace became a count and then a marquis, which are special titles of nobility.

Early Life and Discoveries

A portrait of young Pierre-Simon Laplace.

Many details about Laplace's early life are missing. Records were lost when his family home was burned in 1925. More records were destroyed when his house near Paris was looted in 1871.

Laplace was born in a small village in Normandy, France, on March 23, 1749. His parents were comfortable, and his father was a cider merchant. Young Pierre-Simon went to a local school run by monks. His father wanted him to become a priest.

At 16, Laplace went to the University of Caen to study theology. But he met two math teachers there who sparked his love for mathematics. He quickly showed how brilliant he was. He wrote a paper on integral calculus, which was noticed by the famous mathematician Joseph Louis Lagrange.

Laplace soon realized he didn't want to be a priest. He decided to become a professional mathematician instead. He moved to Paris with a letter of introduction to Jean le Rond d'Alembert, a leading scientist.

One story says d'Alembert gave Laplace a difficult math book and told him to come back after reading it. Laplace returned in a few days, having understood it completely. D'Alembert was so impressed that he took Laplace under his wing. Another story says Laplace solved a hard problem overnight, amazing d'Alembert.

Thanks to d'Alembert, Laplace got a teaching job at the École Militaire. This gave him a steady income and time to focus on his own research. For the next 17 years, he made many important discoveries in astronomy.

The calorimeter used by Laplace and Lavoisier to study heat.

From 1780 to 1784, Laplace worked with the famous French chemist Antoine Lavoisier. They did experiments together, even designing their own equipment. In 1783, they published a paper called Memoir on Heat. In it, they talked about how molecules move and measured the heat capacity of different materials.

Laplace's talent was clear, and he was elected to the French Academy of Sciences in 1773 at just 24 years old. He did most of his scientific work there.

In 1788, at 39, Laplace married Marie-Charlotte de Courty de Romanges, who was 18. They had a son, Charles-Émile, and a daughter, Sophie-Suzanne.

Understanding Ocean Tides

Newton's three-body model, which helped explain forces like tides.

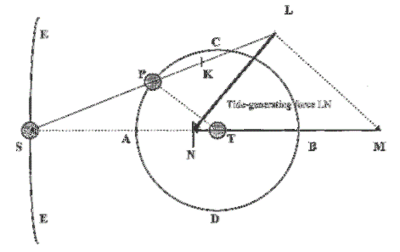
Laplace made huge progress in understanding ocean tides. While earlier scientists like Isaac Newton and Daniel Bernoulli described the forces that cause tides, Laplace's dynamic theory of tides (1775) explained how the oceans actually react to these forces.

His theory considered things like friction, resonance, and the natural periods of ocean basins. It correctly predicted the large amphidromic systems, which are points in the ocean where the tide doesn't change. This helped explain why tides are much higher in some places (up to 15 meters) than what earlier theories predicted (less than half a meter).

Today, satellite observations confirm how accurate Laplace's dynamic theory is. Understanding tides is very important for scientists. It helps them calculate gravity and changes in sea levels accurately, as tidal variations need to be removed from measurements.

Laplace's Tidal Equations

A. How the Moon's gravity affects tides.

B. Another view of the Moon's gravitational effect on tides.

In 1776, Laplace created a set of mathematical equations to describe how tides flow in the ocean. These are called Laplace's tidal equations. They include the Coriolis effect, which is the force caused by the Earth's rotation that deflects moving objects.

These equations are still used today to model and predict tides around the world. They show how the height of the tide and the speed of the water change over time and across the ocean.

Understanding Earth's Shape

Laplace also studied the shape of the Earth and how gravity works. In the 1780s, he published important papers on this topic. He figured out how the gravity of a spheroid (a slightly flattened sphere, like Earth) affects objects outside it.

This work was important because it introduced spherical harmonics (sometimes called Laplace's coefficients) into math. It also developed the idea of the gravitational potential in celestial mechanics.

Spherical Harmonics

Spherical harmonics are used to describe shapes and fields on a sphere.

In 1783, another mathematician, Adrien-Marie Legendre, introduced some special functions. Laplace then expanded on this idea to create a more general set of functions called spherical harmonics.

These functions are very useful because they can describe any pattern or shape on the surface of a sphere. This makes them perfect for mapping the sky or understanding the Earth's gravity.

Potential Theory

Laplace also helped develop the idea of the scalar potential. Imagine gravity pulling on an object. This pull is a vector, meaning it has both strength and direction. A potential function is a simpler, scalar way to describe this force. A scalar only has strength, making it easier to work with.

Laplace used calculus to show that this potential function always follows a specific differential equation called Laplace's equation. This equation is found everywhere in physics, from fluid movement to electromagnetism. It helps scientists understand how forces and fields behave in space.

Planets and Moons

The title page of a book from 1817 about Jupiter's moons, which mentions Laplace's contributions.

Tables from a book about Jupiter's moons, showing calculations influenced by Laplace's discoveries.

Jupiter and Saturn's Movements

Laplace wrote several papers about how planets affect each other's movements. He focused on a long-standing mystery: the "great Jupiter–Saturn inequality." This was a problem in predicting the exact movements of these two giant planets.

Laplace discovered that the problem came from how close their orbits were in terms of time. Two orbits of Saturn around the Sun are almost exactly five orbits of Jupiter. This creates a special effect that makes their gravitational pulls on each other much stronger over long periods. This effect causes small but noticeable changes in their orbits over about 900 years.

Thanks to Laplace's discoveries, scientists could finally make much more accurate tables for the movements of Jupiter and Saturn.

Books on the Solar System

Laplace wanted to write a complete book that would explain all the mechanical problems of the Solar System. He wanted to make the theories match observations so perfectly that no guesswork would be needed in astronomy. This led to two major works: Exposition du système du monde and Mécanique céleste.

His Exposition du système du monde, published in 1796, gave a general overview of how the Solar System works. It also included a history of astronomy. This book was so well-written that it earned him a spot in the French Academy.

In this book, Laplace also developed the nebular hypothesis. This idea, first suggested by others, explains how the Solar System formed. Laplace described it as starting from a giant, hot, spinning cloud of gas. As it cooled, rings broke off, which then cooled and formed the planets. The central part became the Sun. This idea still helps explain how planetary systems form today.

Laplace's detailed mathematical work on the Solar System is in his five-volume Mécanique céleste. The first two volumes (1799) explained how to calculate planet movements and solve tide problems. The next two (1802 and 1805) showed how to use these methods and included astronomical tables. The final volume (1825) was mostly historical, but it also included his latest research.

This massive work was like translating Isaac Newton's Principia into the language of calculus. It also completed parts that Newton couldn't fully explain. It remains a very important book in astronomy.

Black Holes: An Early Idea

Laplace also came very close to imagining the concept of a black hole. He suggested that there could be stars so massive that their gravity would be too strong for even light to escape from their surface. This idea was far ahead of its time and wasn't fully explored until much later.

Arcueil and the Society of Arcueil

Laplace's house at Arcueil to the south of Paris.

In 1806, Laplace bought a house in Arcueil, a village near Paris. His neighbor was the chemist Claude Louis Berthollet. These two scientists became the center of an informal group called the Society of Arcueil.

Because they were close to Napoleon, Laplace and Berthollet had a lot of power in the scientific world. They could influence who got important jobs and who was admitted to prestigious scientific groups.

Understanding Probability and Statistics

In 1812, Laplace published his book Théorie analytique des probabilités (Analytic Theory of Probabilities). In this book, he laid down many basic ideas in statistics. The first part dealt with probability methods, and the second part focused on how to use statistics.

Laplace's work on probability was very important. It helped shape how we understand chance and uncertainty. His book was the most influential on mathematical probability theory until the end of the 19th century.

Inductive Probability

In another book, Essai philosophique sur les probabilités (1814), Laplace explained a mathematical way of using probability for inductive reasoning. This is similar to what we now call Bayesian probability. He started with several principles of probability:

Probability is the number of "favored events" divided by the total number of possible events.
If events are independent, the probability of all of them happening is found by multiplying their individual probabilities.
He also presented what is now known as Bayesian probability, which helps update beliefs based on new evidence.

One famous formula from his system is the rule of succession. Imagine you have a trial with only two outcomes, "success" or "failure." If you don't know much about how likely each outcome is, Laplace's formula helps predict the probability of the next trial being a success:

Probability (next outcome is success) = (number of past successes + 1) / (total number of past trials + 2)

This formula is still used today to estimate probabilities, especially when you have only a small number of observations.

Laplace used a famous example to explain this: the probability that the sun will rise tomorrow, given that it has always risen in the past. He calculated it as (number of past sunrises + 1) / (number of past sunrises + 2). He knew this result might seem strange. He explained that someone who understands the laws of nature would know that nothing could stop the sun from rising.

Least Squares and Central Limit Theorem

Laplace also contributed to the method of least squares, a way to find the "best fit" line for a set of data points. He showed how this method could be justified using probability theory.

He also developed the first general central limit theorem. This theorem is very important in statistics. It says that if you take many random samples from a population, the average of those samples will tend to follow a normal distribution, even if the original population doesn't. This helps scientists make predictions and draw conclusions from data.

Laplace's Demon

Laplace famously imagined an "intelligence" that knew everything about the universe at one moment. This intelligence would know the exact position and speed of every single atom. Because of this, it could calculate everything that would happen in the future and everything that had happened in the past.

This idea is often called Laplace's demon. It suggests that if we knew everything about the present, we could predict the future perfectly. Laplace himself didn't use the word "demon." He simply referred to "an intelligence... Nothing would be uncertain for it, and the future, like the past, would be present to its eyes."

This concept is about causal determinism, the idea that everything that happens is determined by what happened before.

Laplace Transforms

Laplace also developed the Laplace transform. This is a powerful mathematical tool that changes a function of time into a function of a complex variable. It's used to solve many kinds of problems in engineering and physics, especially those involving differential equations.

Other Discoveries

Laplace made many other important contributions to mathematics and science:

He discussed the general theory of determinants, which are numbers that help solve systems of equations.
He proved that every equation with an odd degree must have at least one real quadratic factor.
He developed Laplace's method for estimating integrals.
He worked on solving linear partial differential equations.
In his work on probabilities, he contributed to the de Moivre–Laplace theorem, which links the binomial distribution to the normal distribution.

Surface Tension

Laplace built on the work of Thomas Young to develop the theory of capillary action. This is the way liquids move up narrow tubes or through porous materials. He also helped create the Young–Laplace equation, which describes the pressure difference across a curved liquid surface.

Speed of Sound

In 1816, Laplace was the first to correctly explain why the speed of sound in air is what it is. Earlier theories, like Newton's, gave a value that was too low. Laplace realized that when sound waves travel through air, they cause the air to compress and heat up very quickly. This adiabatic compression affects the speed of sound.

Politics and Public Life

Minister of the Interior

Early in his career, Laplace stayed out of politics. He even left Paris during the most violent parts of the French Revolution.

In November 1799, after Napoleon took power, he appointed Laplace as the Minister of the Interior. However, this job only lasted six weeks. Napoleon's brother, Lucien Bonaparte, took over. It seems Laplace was appointed as a temporary figurehead while Napoleon secured his power.

From Napoleon to the Kings

Laplace.

Even though he was removed from office, Napoleon wanted to keep Laplace's support. He made Laplace a senator. In his book Mécanique céleste, Laplace added a note expressing his devotion to Napoleon. However, after the Bourbon Restoration (when the kings returned to power), this note was removed from later copies of the book.

In 1814, when Napoleon's empire was falling, Laplace quickly offered his support to the new royal government. In 1817, he was rewarded with the title of marquis. Some people criticized Laplace for changing his loyalty so easily. However, his scientific knowledge was very useful on many government committees, which likely helped overlook his political changes.

Historians debate whether Laplace was truly an opportunist. Some suggest that after Napoleon's disastrous Russian campaign, Laplace, like many others, became worried about the country's future. His only daughter had died, and his son was fighting in the war. Napoleon's insensitive comments about his daughter's death also strained their relationship.

Political Philosophy

In the second edition of his Essai philosophique (1814), Laplace shared some thoughts on politics and government. He believed that the stability found in nature, which science revealed, could be a model for how human societies should be governed to ensure their survival.

He also showed how probability could be used in political studies. For example, he applied the law of large numbers to explain why the Borda count voting method, used to elect members of the Academy of Sciences, was fair.

Death and Legacy

Tomb of Pierre-Simon Laplace.

Pierre-Simon Laplace died in Paris on March 5, 1827. His brain was removed by his doctor and kept for many years. It was reportedly smaller than an average brain. Laplace was buried in Paris, but his remains were later moved to his family estate in Saint Julien de Mailloc, Normandy, France. His tomb is on a hill overlooking the village.

Religious Views

Laplace's views on religion have been debated. He was raised Catholic, but as an adult, he seemed to lean towards deism. Deists believe in a God who created the universe but does not interfere with its workings. Some of his friends thought he was an atheist (someone who doesn't believe in God), while others described him as agnostic (someone who believes we can't know if God exists).

I had no need of that hypothesis

There's a famous story about Laplace and Napoleon. Napoleon supposedly asked Laplace why he didn't mention God in his book about astronomy. Laplace is said to have replied, "I had no need of that hypothesis."

However, this story might not be entirely accurate. Some historians believe Laplace did say something similar, but not directly about God's existence. Instead, it might have been about not needing a "God of the gaps" explanation for things that science could explain. Stephen Hawking suggested that Laplace wasn't saying God didn't exist, but that God didn't need to break the laws of science to make the universe work.

Laplace himself wrote that the amazing arrangement of the Sun, planets, and comets could be explained by the laws of motion. He agreed with Gottfried Wilhelm Leibniz's idea that it was "narrow-minded" to think God made the universe so poorly that he had to constantly fix it.

In some private writings, Laplace criticized miracles and religious doctrines, saying they went against reason and the laws of nature. He also made fun of using probability in theology.

In his old age, Laplace still discussed Christianity. He praised its positive influence but held firm to his belief that the unchanging laws of nature didn't allow for supernatural events.

Honors and Recognition

Laplace received many honors for his incredible contributions to science:

He was a member of the Royal Institute of the Netherlands (1809).
He was an honorary member of the American Academy of Arts and Sciences (1822).
The asteroid 4628 Laplace is named after him.
A mountain on the Moon is called Promontorium Laplace.
His name is one of the 72 names inscribed on the Eiffel Tower in Paris.
A train station in Arcueil, France, bears his name.

Famous Sayings

"I had no need of that hypothesis." (Allegedly to Napoleon about God in his astronomy book.)
"It is therefore obvious that..." (Often used in Celestial Mechanics when he had a proof but found it too long or complicated to write out.)
"The weight of evidence for an extraordinary claim must be proportioned to its strangeness." (This means that if something is very unusual, you need very strong proof.)
"Infinitely varied in her effects, nature is only simple in her causes."
"What we know is little, and what we are ignorant of is immense."
"One sees in this essay that the theory of probabilities is basically only common sense reduced to a calculus."

List of Works

(in fr) Traité de mécanique céleste. 1. Paris: Charles Crapelet. 1799. https://gutenberg.beic.it/webclient/DeliveryManager?pid=12217993.
(in fr) Traité de mécanique céleste. 2. Paris: Charles Crapelet. 1799. https://gutenberg.beic.it/webclient/DeliveryManager?pid=12219220.
(in fr) Traité de mécanique céleste. 3. Paris: Charles Crapelet. 1802. https://gutenberg.beic.it/webclient/DeliveryManager?pid=12220405.
(in fr) Traité de mécanique céleste. 4. Paris: Charles Crapelet. 1805. https://gutenberg.beic.it/webclient/DeliveryManager?pid=12221428.
(in fr) Traité de mécanique céleste. 5. Paris: Charles Louis Étienne Bachelier. 1852. https://gutenberg.beic.it/webclient/DeliveryManager?pid=12222637.
(in it) Précis de l'histoire de l'astronomie. Milano: Angelo Stanislao Brambilla. 1823. https://gutenberg.beic.it/webclient/DeliveryManager?pid=12414013.
(in fr) Exposition du système du monde. Paris: Charles Louis Étienne Bachelier. 1824. https://gutenberg.beic.it/webclient/DeliveryManager?pid=3903942.

Volumes 1-5 of Pierre-Simon Laplace's "Traité de mécanique céleste" (1799)
Title page to Volume I of "Traité de mécanique céleste" (1799)
Table of contents to Volume I of "Traité de mécanique céleste" (1799)
First page of Volume I of "Traité de mécanique céleste" (1799)