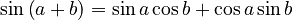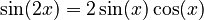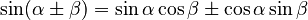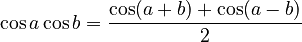History of trigonometry facts for kids
Trigonometry is a branch of mathematics that studies the relationships between the sides and angles of triangles. It's super useful for measuring distances and heights, like how tall a mountain is or how far away a star is!
People started studying triangles way back in ancient times, around 2000 BC, in places like Ancient Egypt and Babylonia. Later, in ancient Greece, mathematicians began to study these relationships more deeply.
Over time, this knowledge spread to India, where smart thinkers like Aryabhata (around 500 AD) discovered important ideas like the sine and cosine functions.
During the Middle Ages, mathematicians in the Islamic world continued to develop trigonometry. They made it its own subject and learned about all six main trigonometric functions. Thanks to their work, trigonometry eventually came to Europe during the Renaissance.
In more recent times, brilliant minds like Isaac Newton and Leonhard Euler helped shape trigonometry into the modern form we know today.
Contents
- Where Did the Word "Trigonometry" Come From?
- Ancient Discoveries in Trigonometry
- Modern Trigonometry
- See also
Where Did the Word "Trigonometry" Come From?
The word "trigonometry" comes from two old Greek words:
- trigōnon, which means "triangle"
- metron, which means "measure"
So, trigonometry literally means "triangle measuring"!
The words "sine" and "cosine" actually came from a mistake in translation! They came from the Latin word sinus, which means "bay" or "curve," after a mix-up from an Arabic word.
The word tangent comes from the Latin word tangens, meaning "touching." Think of a line that just touches a circle.
Secant comes from the Latin word secans, meaning "cutting," because a secant line cuts through a circle.
The "co-" part in "cosine," "cotangent," and "cosecant" means "complementary." It refers to the angle that completes a right angle (90 degrees).
Even the words "minute" and "second" (when talking about angles) come from Latin! They mean "first small parts" and "second small parts."
Ancient Discoveries in Trigonometry
Early Beginnings in the Near East
Ancient Egyptians and Babylonians knew a lot about how the sides of similar triangles related to each other. But they didn't have the idea of measuring angles like we do today.
Egyptian Pyramid Builders
The Egyptians used a basic form of trigonometry when building their amazing pyramids. A very old document called the Rhind Mathematical Papyrus (from around 1600 BC) has a problem about a pyramid:
"If a pyramid is 250 cubits high and the side of its base 360 cubits long, what is its seked?"
The "seked" was a ratio that helped them figure out the slope of the pyramid's face. It was like the "run-to-rise" ratio, which is similar to what we call the cotangent of the angle today.
Babylonian Star Gazers
Babylonian astronomers kept detailed records of stars and planets. They needed to measure angular distances in the sky. Some people think an ancient Babylonian tablet called Plimpton 322 (from about 1900 BC) might even be an early trigonometry table, but this is still debated by historians.
Greek and Hellenistic Contributions
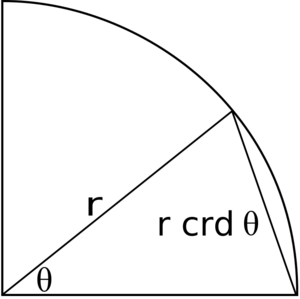
Ancient Greek mathematicians used something called a "chord." Imagine a circle and an arc on it. The chord is the straight line connecting the two ends of that arc.
They knew that if you cut a chord in half, that half is related to what we now call the sine of half the angle. Because of this, many trigonometric ideas we use today were known to them, but in terms of chords.
Euclid and Archimedes' Hidden Trigonometry
Even though famous mathematicians like Euclid and Archimedes didn't use the word "trigonometry," their works contained ideas that are the same as modern trigonometric laws. For example, some parts of Euclid's Elements are like the laws of cosines and law of sines.
Hipparchus: The Father of Trigonometry
Hipparchus of Nicaea (around 180 – 125 BCE) is often called "the father of trigonometry." He was probably the first to create a table that showed the relationship between angles and their chords. This was a huge step!
It's believed that Hipparchus also helped popularize the idea of dividing a circle into 360 degrees. This idea might have come from Babylonian astronomy, where they divided the day into 360 parts. Each degree is then divided into 60 minutes, and each minute into 60 seconds, thanks to the Babylonian sexagesimal (base-60) number system.
Ptolemy's Almagest
Claudius Ptolemy (around 90 – 168 AD) built on Hipparchus's work in his famous book, the Almagest. This book was mainly about astronomy, and astronomy needs a lot of trigonometry!
Ptolemy's table showed the lengths of chords for a circle with a diameter of 120 units, for angles from 0.5 to 180 degrees. He also used a special rule called Ptolemy's theorem to calculate these chords. This theorem is similar to our modern formulas for the sine and cosine of sums and differences of angles.
Indian Mathematics: Sine and Cosine Emerge
Some of the most important developments in trigonometry happened in India. In works from the 4th-5th century AD, like the Surya Siddhanta, the sine function was clearly defined as the relationship between half an angle and half a chord. They also defined cosine, versine, and inverse sine.
Soon after, the Indian mathematician Aryabhata (476–550 AD) wrote the Aryabhatiya. This book contains the earliest surviving tables of sine and versine values, calculated for every 3.75 degrees, with great accuracy. The Indian words for sine and cosine, jya and kojya, eventually became "sine" and "cosine" after being translated.
Later Indian Discoveries
In the 7th century, Bhaskara I created a formula to calculate the sine of an angle without needing a table. Later, Brahmagupta (also 7th century) rediscovered important formulas relating sine and cosine.
Bhaskara II in the 12th century made big advances in spherical trigonometry (trigonometry on the surface of a sphere). He was one of the first to discover formulas for the sine of the sum and difference of two angles, like:
Madhava (around 1400) was a pioneer in using infinite series for trigonometric functions. He developed the ideas of power series and Taylor series and used them to find very accurate values for sine, cosine, tangent, and arctangent. He even made sine tables accurate to 12 decimal places!
Chinese Contributions to Trigonometry

In China, Aryabhata's sine tables were translated in 718 AD. While the Chinese were great at other areas of mathematics, trigonometry wasn't as widely used as in other parts of the world at first. They used a practical method called chong cha.
However, this started to change during the Song dynasty (960–1279). Chinese mathematicians began to see how important spherical trigonometry was for astronomy and calendars.
Shen Kuo (1031–1095), a brilliant Chinese scientist, used trigonometric functions to solve problems involving circles. Later, Guo Shoujing (1231–1316) used spherical trigonometry to improve the Chinese calendar system.
Medieval Islamic World: A Golden Age for Trigonometry

During the Islamic Golden Age, Muslim mathematicians greatly expanded on earlier works. They made trigonometry its own independent subject, separate from astronomy. This is when "the first real trigonometry emerged," focusing on the study of triangles themselves.
Early on, astronomers used complex methods to calculate the positions of the moon and stars for the Islamic calendar. But these methods were difficult. So, they looked for simpler ways.
Key Islamic Mathematicians
- In the early 9th century, Muhammad ibn Mūsā al-Khwārizmī created accurate sine and cosine tables and the first table of tangents. He also pioneered spherical trigonometry.
- Habash al-Hasib al-Marwazi (830 AD) made the first table of cotangents.
- Muhammad ibn Jābir al-Harrānī al-Battānī (853-929 AD) discovered the secant and cosecant functions and made tables for them.
By the 10th century, Abū al-Wafā' al-Būzjānī was using all six trigonometric functions. He had very accurate sine tables and discovered important formulas like:
He also discovered the law of sines for spherical triangles.
Ibn Yunus (late 10th/early 11th century) discovered another important trigonometric identity:
Al-Jayyani (989–1079) wrote the first book specifically on spherical trigonometry. His work influenced European mathematicians.
Triangulation and Independent Discipline
Muslim mathematicians were the first to develop triangulation, a method used to measure distances by forming triangles. Abu Rayhan Biruni used it in the early 11th century to measure the size of the Earth and distances between places.
In the 13th century, Nasīr al-Dīn al-Tūsī was the first to treat trigonometry as a mathematical subject on its own, separate from astronomy. He developed spherical trigonometry into the form we know today and stated the law of sines and the law of tangents. He is often called the creator of trigonometry as an independent math field.
In the 15th century, Jamshīd al-Kāshī clearly stated the law of cosines, which is still called "Al-Kashi's theorem" in France. He also made very accurate trigonometric tables.
Modern Trigonometry
European Renaissance and Beyond
In 1342, Gersonides (Levi ben Gershon) wrote a book on sines, chords, and arcs, proving the sine law for flat triangles.
Sailors in the Mediterranean Sea used a simplified trigonometric table called the "toleta de marteloio" in the 14th-15th centuries to help with navigation.
Regiomontanus was likely the first European mathematician to treat trigonometry as a separate subject in his book De triangulis omnimodis (1464).
Georg Joachim Rheticus (a student of Copernicus) was probably the first in Europe to define trigonometric functions directly using right triangles instead of circles.
In the 17th century, Isaac Newton and James Stirling developed general formulas for trigonometric functions.
The 18th century saw Leonhard Euler's important work, Introduction in analysin infinitorum (1748). He helped establish the modern way of looking at trigonometric functions, deriving their infinite series and presenting "Euler's formula" (eix = cos x + i sin x). Euler also used the abbreviations for sine, cosine, tangent, etc., that we use today.
Other mathematicians like Brook Taylor, James Gregory, and Colin Maclaurin also made big contributions to the development of trigonometric series in the 17th and 18th centuries.
See also
 In Spanish: Historia de la trigonometría para niños
In Spanish: Historia de la trigonometría para niños
- Greek mathematics
- History of mathematics
- Trigonometric functions
- Trigonometry
- Ptolemy's table of chords
- Aryabhata's sine table