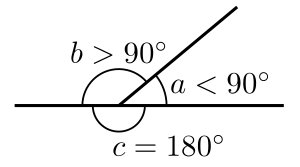Geometry facts for kids
Geometry is a part of mathematics. It helps us understand the size, shapes, and positions of objects. We study both flat (2D) shapes and solid (3D) shapes in geometry.
Squares, circles, and triangles are some simple flat shapes. Cubes, cylinders, cones, and spheres are simple solid shapes.
Contents
Why is Geometry Useful?
Geometry helps us measure things. For flat shapes, we can find their area (how much surface they cover) and perimeter (the distance around their edge). For solid shapes, we can find their volume (how much space they take up) and surface area (the total area of their outside surfaces).
Geometry helps people figure out many things, like:
- The surface area of a house, to buy the right amount of paint.
- The volume of a box, to see if it can hold a liter of food.
- The area of a farm, so it can be divided into equal parts.
- The distance around a pond, to know how much fencing to buy.
Where Did Geometry Come From?
Geometry started a long, long time ago. People used it to measure and divide land fairly. The word "geometry" actually means "to measure the land."
Over time, it grew into a very important part of mathematics. The ancient Greek mathematician Euclid wrote one of the first and most famous books about geometry. Geometry is one of the oldest types of mathematics we know!
Basic Ideas in Geometry
Geometry begins with a few simple ideas that we accept as true. These are called axioms. Here are some examples:
What is a Point?
A point is like a tiny dot you make with a pencil on paper. It shows a specific location, but it has no size at all.
What is a Line?
A straight line is the shortest distance between two points. Imagine pulling a tight string between two spots; that's a straight line. A line goes on forever in both directions.
What is a Plane?
A plane is a flat surface that goes on forever in all directions. Think of a perfectly flat wall that never ends.
Important Concepts in Geometry
Here are some other important ideas in geometry.
Axioms and Rules
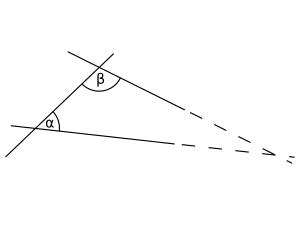
Euclid used a special way to teach geometry in his book, Elements. He started with basic rules, called axioms or postulates, that seemed true without needing proof. Then, he used mathematical reasoning to prove other properties. This way of thinking is called axiomatic geometry.
Later, in the 1800s, mathematicians like Nikolai Ivanovich Lobachevsky, János Bolyai, and Carl Friedrich Gauss discovered new types of geometry called non-Euclidean geometries. These new geometries showed that Euclid's rules were not the only way to describe space.
Lines and Curves
Euclid described a line as "length without breadth." In modern math, a line can be defined in different ways depending on the type of geometry. For example, in analytic geometry, a line on a flat surface is often described by an linear equation.
A curve is a 1-dimensional shape. It can be straight, like a line, or it can bend. Curves on a flat surface are called plane curves. Curves in 3D space are called space curves.
Angles
Euclid said a plane angle is formed when two lines meet but don't lie straight with each other. Today, we say an angle is made by two rays (parts of a line that start at one point and go forever in one direction) that share a common starting point called the vertex.
In Euclidean geometry, angles help us study shapes like polygons and triangles. The study of angles in triangles and circles is the basis of trigonometry, which is used in many fields like engineering and physics.
Surfaces
A surface is a two-dimensional object, like the outside of a sphere or a paraboloid. Think of the skin of an apple or the top of a table.
Dimensions
Traditional geometry usually deals with 1D (a line), 2D (a plane), and 3D (our everyday world). But mathematicians have explored higher dimensions for a long time. For example, string theory in physics uses 10 or 11 dimensions!
Symmetry

Symmetry is a very old idea in geometry. Shapes like the circle, regular polygons, and platonic solids (like a cube) are very symmetric and were important to ancient thinkers.
Symmetry is everywhere, from patterns in nature to art. In the late 1800s, a mathematician named Felix Klein showed that symmetry is a key idea in understanding what geometry is all about.
Images for kids
-
Woman teaching geometry. Illustration at the beginning of a medieval translation of Euclid's Elements, (c. 1310).
-
Quintic Calabi–Yau threefold
See also
 In Spanish: Geometría para niños
In Spanish: Geometría para niños
 | John T. Biggers |
 | Thomas Blackshear |
 | Mark Bradford |
 | Beverly Buchanan |