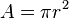Euclidean plane facts for kids
In mathematics, a Euclidean plane is a flat, two-dimensional surface. Think of it like a perfectly flat piece of paper that goes on forever in all directions. It's a basic geometric space where you need two real numbers to find the spot of any point.
This plane has special features. For example, it includes the idea of parallel lines, which are lines that never meet. It also has ways to measure things, like distance, which helps us draw circles and measure angles.
When we add a special grid system, called a Cartesian coordinate system, to a Euclidean plane, we call it a Cartesian plane. This grid helps us locate points using numbers.
Contents
History of the Plane
The idea of the Euclidean plane goes way back to ancient Greece. Euclid, a famous mathematician, wrote about two-dimensional shapes in his books called Euclid's Elements. He explored ideas like how shapes can be similar, the Pythagorean theorem (about right triangles), and how to measure areas.
Later, in the 1600s, mathematicians like René Descartes and Pierre de Fermat came up with a new way to describe the plane. They created the Cartesian coordinate system. This system uses two fixed, perpendicular (at right angles) lines, called coordinate axes. These axes cross at a point called the origin, usually marked as (0, 0).
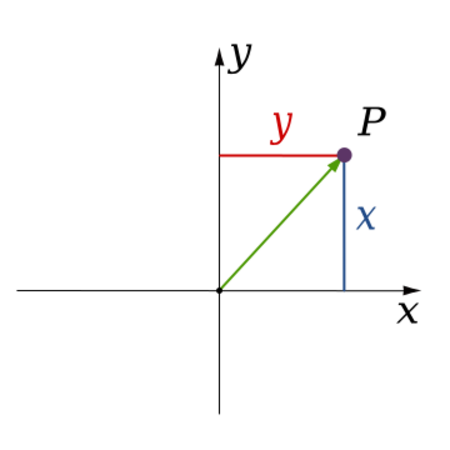
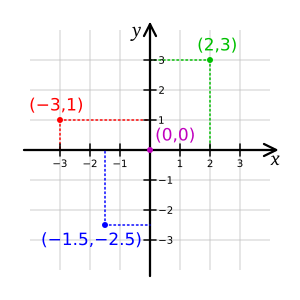
With this system, you can find any point on the plane using two numbers. These numbers tell you how far the point is from each axis. For example, a point might be (3, 5), meaning it's 3 units along one axis and 5 units along the other. This made it much easier to study shapes and equations.
Even later, the plane was seen as a "complex plane". This was a way to work with complex numbers, which are numbers that include the square root of negative one. These ideas were developed by people like Caspar Wessel and Jean-Robert Argand.
The Plane in Geometry
Coordinate Systems
In analytic geometry, which is also called Cartesian geometry, we describe every point on a two-dimensional surface using two coordinates. We use two axes, usually labeled x and y, that cross at the origin. The position of any point is given by a pair of numbers, like (x, y). Each number tells you the distance of that point from the origin along its specific axis.
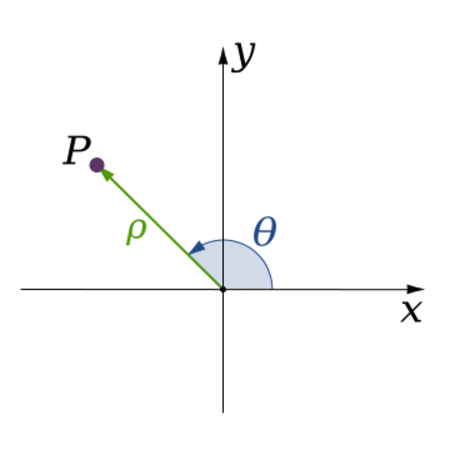
Another common way to find points is using the polar coordinate system. Instead of x and y distances, this system uses a point's distance from the origin and its angle from a starting line.
-
A Cartesian coordinate system uses X and Y axes.
-
A Polar coordinate system uses distance and angle.
Polygons: Shapes on the Plane
In two dimensions, there are many different shapes called polygons. Polygons are closed shapes made of straight lines. Here are some common regular polygons, where all sides and angles are equal:
| Name | Triangle | Square | Pentagon | Hexagon | Heptagon | Octagon |
|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 |
 |
There are also star polygons, which are non-convex (meaning they "dent in") and have points like stars. An example is a pentagram.
Circles
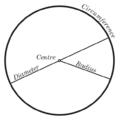
A circle is another important shape on a Euclidean plane. It's a shape where all points are the same distance from a central point. The distance around a circle is called its circumference, and the space it covers is its area.
The area of a circle is found using the formula:
Here,  is the radius (the distance from the center to any point on the circle), and
is the radius (the distance from the center to any point on the circle), and 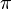 (pi) is a special number, about 3.14159.
(pi) is a special number, about 3.14159.
Other Shapes
Besides polygons and circles, there are many other curved shapes you can find on a two-dimensional plane. Some important ones are the conic sections: the ellipse (an oval shape), the parabola (a U-shaped curve), and the hyperbola (two separate curves).
The Plane in Graph Theory
In graph theory, a planar graph is a special kind of graph that can be drawn on a flat surface (like our Euclidean plane) without any of its lines (called "edges") crossing each other. Imagine drawing a network of cities and roads. If you can draw all the roads without any of them overlapping, then it's a planar graph!
Images for kids
-
A Monogon
-
A Digon
-
A Heptagram {7/2}
-
A Heptagram {7/3}
-
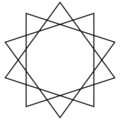
An Octagram
-
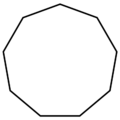
A Nonagon
-
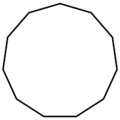
A Decagon
-
An Octadecagon
-
An Enneadecagon
-
An Icosagon
See also
 In Spanish: Plano (geometría) para niños
In Spanish: Plano (geometría) para niños
- Geometric space
- Picture function
- Planimetrics