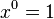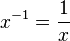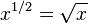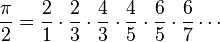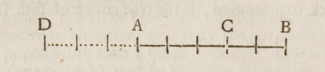John Wallis facts for kids
Quick facts for kids
John Wallis
|
|
|---|---|
 |
|
| Born | 3 December [O.S. 23 November] 1616 Ashford, Kent, England
|
| Died | 8 November 1703 (aged 86) [O.S. 28 October 1703] Oxford, Oxfordshire, England
|
| Nationality | English |
| Education | Felsted School, Emmanuel College, Cambridge |
| Known for | Wallis product Inventing the symbol ∞ Extending Cavalieri's quadrature formula Coining the term "momentum" |
| Scientific career | |
| Fields | Mathematics |
| Institutions | |
| Academic advisors | William Oughtred |
| Notable students | William Brouncker |
John Wallis (born December 3, 1616 – died November 8, 1703) was an English clergyman and a brilliant mathematician. He is partly credited with developing calculus, a very advanced type of math.
From 1643 to 1689, he worked as the main code-breaker for the English Parliament and later for the King's court. He is famous for introducing the symbol ∞ to represent infinity. He also used the symbol 1/∞ for a very, very tiny number, almost zero. John Wallis lived at the same time as Isaac Newton and was one of the most important thinkers in early modern mathematics.
Contents
About John Wallis
Early Life and Education
John Wallis was born in Ashford, Kent, England. He was one of five children. When he was nine, he moved to a different school in Tenterden because of an outbreak of the plague.
In 1631, at Felsted School, Wallis first discovered mathematics. He really enjoyed it, even though math wasn't seen as a serious academic subject back then. It was considered more of a practical skill. At Felsted, he became very good at speaking and writing Latin. He also learned French, Greek, and Hebrew.
In 1632, he went to Emmanuel College, Cambridge, planning to become a doctor. While there, he publicly discussed the idea of blood circulating in the body, which was a new and exciting theory at the time. However, his main interest was always mathematics. He earned his first degree in 1637 and a master's degree in 1640. After that, he became a priest.
Family Life
On March 14, 1645, John Wallis married Susanna Glynde. They had three children:
- Anne Blencoe (born 1656 – died 1718): She married Sir John Blencowe in 1675 and had children.
- John Wallis (born 1650 – died 1717): He became a Member of Parliament. He married Elizabeth Harris in 1682 and had one son and two daughters.
- Elizabeth Wallis (born 1658 – died 1703): She married William Benson but did not have any children.
Career and Achievements
Wallis supported the Parliament during the English Civil War. He helped them a lot by deciphering secret messages from the Royalists. At that time, code-breaking was tricky. Wallis understood that codes based on a changing key were much safer than those based on a secret method. He even called them "unbreakable."
After returning to London, Wallis joined a group of scientists who later formed the famous Royal Society. This allowed him to focus on his love for mathematics. He quickly mastered important math books and began writing his own. He wrote the first survey in England about mathematical ideas, including the Hindu-Arabic number system.
In 1649, Wallis was chosen to be the Savilian Professor of Geometry at Oxford University. He held this important position for 54 years until his death. Even though he was chosen partly for political reasons, his work at Oxford proved how talented he was. In 1650, he became a minister.
Besides math, Wallis also wrote about theology (the study of religion), logic, English grammar, and philosophy. He even helped create a system to teach a deaf boy how to speak.
Amazing Math Contributions
John Wallis made big contributions to many areas of math, including trigonometry, calculus, geometry, and infinite series (long lists of numbers). In one of his books, he introduced the term "continued fraction".
Understanding Shapes with Math
In 1655, Wallis published a book about conic sections (shapes like circles, ellipses, and parabolas). He showed how to describe these curves using mathematical equations. This helped make René Descartes' ideas about analytic geometry easier to understand.
In this book, Wallis also made the symbol ∞ popular for infinity. He explained that you could think of a flat surface as being made of an "infinite number of parallel lines." He used 1/∞ to mean an "infinitely small part."
Calculus and Areas
Wallis's most important work, Arithmetica Infinitorum (meaning "Arithmetic of Infinites"), came out in 1656. In this book, he improved and expanded on methods used by other mathematicians like Descartes.
He developed the standard way to write powers of numbers, extending them from whole numbers to rational numbers (fractions). For example, he showed:
He then used integration to find the area under curves. He showed that the area under a curve like y = xm is related to the area of a rectangle by the ratio 1/(m + 1). This was a big step in calculus.
Wallis also worked on finding the area of a circle. He couldn't find the exact area because he didn't know about the binomial theorem yet. But he came up with a very famous formula called the Wallis product, which helps calculate π:
Collisions and Motion
In 1668, the Royal Society asked mathematicians to study how objects collide. Wallis, along with Christopher Wren and Christiaan Huygens, found correct solutions. Their solutions all used the idea of conservation of momentum, which means that the total momentum of objects stays the same before and after a collision. Wallis was special because he also looked at collisions where objects weren't perfectly bouncy (inelastic collision).
Algebra and Number Lines
In 1685, Wallis published a book called Algebra. It included a history of algebra and was important because it was the first time formulas were used in a systematic way. He showed how to represent amounts using numbers, like s = vt for distance, speed, and time.
Wallis is also known for creating the idea of the number line to show negative numbers. He used it to explain how negative numbers are real and useful.
Geometry and Triangles
Wallis is often given credit for proving the Pythagorean theorem using similar triangles. He was also inspired by the work of an Islamic mathematician, Sadr al-Tusi, who wrote about the parallel postulate (a basic rule in geometry). Wallis tried to prove this postulate using similar triangles, but it's now known that it cannot be proven from Euclid's other rules.
Wallis found that Euclid's fifth postulate is the same as what is now called the "Wallis postulate." This postulate says that "On a given finite straight line it is always possible to construct a triangle similar to a given triangle."
Mental Math Skills
Wallis had an amazing ability to do math in his head. He often couldn't sleep, so he would do mental calculations in bed. One night, he calculated the square root of a 53-digit number in his head! The next morning, he wrote down the 27-digit answer, still from memory. This was considered such an incredible feat that it was discussed in the Philosophical Transactions of the Royal Society in 1685.
Other Interests
Wallis also translated ancient Greek works on musical theory into Latin. He wrote about equal temperament, a way of tuning musical instruments that was becoming popular in England.
His book Institutio logicae (on logic) was very popular. He also wrote Grammatica linguae Anglicanae, a book on English grammar that was used for many years.
See also
 In Spanish: John Wallis para niños
In Spanish: John Wallis para niños
- 31982 Johnwallis, an asteroid named after him
- Invisible College
- John Wallis Academy – a school in Ashford renamed in 2010
- Wallis's conical edge
- Wallis' integrals