History of geometry facts for kids

A page from the 1728 Cyclopaedia showing a table about geometry.

Geometry is a very old part of mathematics that studies shapes, sizes, positions, and properties of space. The word "geometry" comes from ancient Greek words meaning "earth measurement." It started because people needed to measure land, build things, and understand the stars.

For a long time, geometry was mostly about using a compass and straightedge to draw perfect shapes. A mathematician named Euclid changed geometry forever. He created a system where all geometric facts could be proven using a few basic rules, called axioms. His famous book, The Elements, was used for over 2,000 years!

Today, geometry is much more complex. It uses advanced math like calculus and abstract algebra. This means modern geometry can look very different from the geometry of ancient times.

Early Geometry

The first signs of geometry come from ancient civilizations like the Indus Valley and Babylonia. This was around 3000 BC. Early geometry was a collection of practical rules. People used them to measure lengths, angles, areas, and volumes. These rules helped with surveying land, building, and astronomy.

Some of these ancient rules were quite advanced. For example, the Egyptians and Babylonians knew about the Pythagorean theorem about 1500 years before Pythagoras. The Egyptians even had a correct way to find the volume of a frustum (a pyramid with its top cut off).

Egyptian Geometry

The ancient Egyptians had ways to estimate the area of a circle. They used a rule that said the area was roughly the square of 8/9 of the circle's diameter. This meant their value for $π$ was about 3.16. This was close, but not as accurate as the Babylonians.

One ancient papyrus, the Moscow Mathematical Papyrus, shows how Egyptians found the volume of a pyramid frustum. They used this formula: 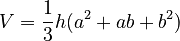$V = \frac{1}{3} h(a^2 + ab + b^2)$ Here, a and b are the lengths of the base and top sides, and h is the height.

Babylonian Geometry

The Babylonians also had rules for areas and volumes. They often estimated the circumference of a circle as three times its diameter. This means they used 3 as an estimate for $π$ . They also knew the Pythagorean theorem.

A recent discovery showed that ancient Babylonians might have used advanced geometry to study the stars. This was about 1400 years before Europeans did.

Vedic Indian Geometry

A page from the Rigveda, an ancient Indian text.

Ancient India, during the Vedic period, also had its own geometry. It was mostly used for building special altars. Early Indian texts like the Śulba Sūtras describe these geometric ideas.

The Śulba Sūtras contain the earliest known written ideas of the Pythagorean Theorem. They show how to use "Pythagorean triples." These are sets of three whole numbers that fit the theorem (like 3, 4, 5).

Historians believe that ancient Indians had a good understanding of these concepts. However, their writings mostly focused on practical uses, like building altars.

Greek Geometry

The ancient Greeks greatly advanced geometry. They focused on proving geometric ideas using logic.

Thales and Pythagoras

The Pythagorean theorem: a² + b² = c²

Thales (around 635-543 BC) was one of the first to use logical proofs in mathematics. He proved five geometry ideas, though his proofs are now lost.

Pythagoras (around 582-496 BC) might have been Thales' student. He traveled to Babylon and Egypt. The famous Pythagorean theorem is named after him. He probably gave one of the first logical proofs for it. Pythagoras and his students discovered many geometry ideas that are still taught today. They also found out about irrational numbers, which are numbers that cannot be written as simple fractions.

Plato

Plato (427-347 BC) was a famous Greek philosopher. He believed that geometry was very important. He thought geometry should only use a compass and a straightedge. He felt that measuring tools like rulers were not for scholars.

This idea led to a deep study of what could be built with just these two tools. Three famous problems came from this:

How to divide an angle into three equal parts.
How to build a cube twice the volume of another cube.
How to build a square with the same area as a given circle.

It was later proven that these constructions are impossible with only a compass and straightedge.

Aristotle (384-322 BC), Plato's student, wrote about logical reasoning. His work helped shape how proofs are done in geometry.

Hellenistic Geometry

Euclid

A statue of Euclid at the Oxford University Museum of Natural History.

An old drawing (around 1310) showing a woman teaching geometry from Euclid's Elements.

Euclid (around 325-265 BC) lived in Alexandria, Egypt. He wrote The Elements of Geometry, a book with 13 chapters. In it, he presented geometry in a perfect logical way, which we now call Euclidean geometry. This book was so good that other geometry textbooks from that time were forgotten.

The Elements started with basic definitions and rules. These rules were called axioms or postulates. From these few rules, all other geometry ideas could be proven. Here are his five main axioms, explained simply:

Any two points can be connected by a straight line.
Any straight line can be made longer in a straight line.
You can draw a circle with any center and any size (radius).
All right angles are equal to each other.
If two lines are crossed by another line, and the angles on one side add up to less than two right angles, then those two lines will eventually meet on that side. This is also called the parallel postulate.

Euclid also used geometry to explain ideas that we now understand as algebra. This is sometimes called "Greek geometric algebra."

Archimedes

Archimedes (287-212 BC) was a very famous mathematician from Syracuse, Sicily. He is known for his Archimedes’ principle about floating objects. He also did important work in geometry, like measuring the area of a circle and the volumes of shapes like cones. His ideas greatly influenced later mathematicians.

After Archimedes

After Archimedes, Greek mathematics slowly declined. Proclus (410-485) was one of the last important Greek geometers. He wrote helpful comments on earlier works, which helped save some of that knowledge.

The famous Library of Alexandria was eventually destroyed. This happened over time due to several events, including conflicts and a decrease in interest in non-religious studies. This loss meant many ancient texts and much knowledge were lost forever.

Classical Indian Geometry

Indian mathematicians also made important contributions to geometry. The Bakhshali manuscript contains geometry problems, including how to find volumes of unusual shapes. It also used a decimal system with a symbol for zero.

Aryabhata's book Aryabhatiya (499 AD) included ways to calculate areas and volumes.

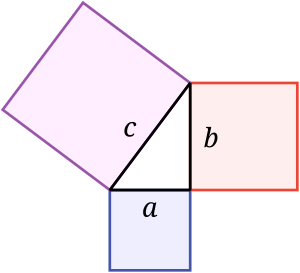
Brahmagupta wrote his book Brāhma Sphuṭa Siddhānta in 628 AD. It had sections on basic math and practical math, including geometry. He shared a famous theorem about cyclic quadrilaterals (shapes with four sides that fit inside a circle).

Brahmagupta's theorem: If a cyclic quadrilateral has diagonals that cross at a right angle, then a line drawn from where the diagonals meet to any side will always cut the opposite side in half.

He also gave a formula for the area of a cyclic quadrilateral: 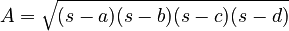$A = \sqrt{(s-a)(s-b)(s-c)(s-d)}$ Here, a, b, c, d are the side lengths, and s is half of the total perimeter.

Parameshvara Nambudiri was the first to give a formula for the radius of the circle that goes around a cyclic quadrilateral.

Chinese Geometry

The Nine Chapters on the Mathematical Art, an important Chinese math book from the 3rd century AD.

A drawing from the Chinese book Haidao Suanjing (3rd century), showing how to survey a sea island.

The earliest known geometry book in China is the Mo Jing, written around 330 BC. It described many ideas in physical science and mathematics. It even defined a geometric point as the smallest part of a line that cannot be divided further. The book also defined circumference, diameter, radius, and volume.

During the Han Dynasty (202 BC-220 AD), mathematics grew. Zhang Heng (78-139 AD) used geometry to solve problems. He tried to find a more accurate value for $π$ . Later, Zu Chongzhi (429-500 AD) made pi even more accurate, between 3.1415926 and 3.1415927.

The Nine Chapters on the Mathematical Art

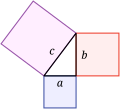
The Nine Chapters on the Mathematical Art was a very important Chinese math book. It was edited by Liu Hui in the 3rd century AD. This book had many geometry problems. It showed how to find areas of squares and circles, and volumes of 3D shapes. It also included the Pythagorean theorem with a proof.

Liu Hui calculated pi as 3.14159 using a polygon with 3072 sides. He also wrote about how to use math for surveying to measure distances, heights, and areas. He explained how complex shapes could be broken down into simpler ones.

The Nine Chapters listed many geometric formulas known by the Han Dynasty, including areas for:

Squares, rectangles, circles
Triangles, trapezoids
Parts of circles (segments, rings)

And volumes for:

Cubes, prisms, pyramids
Frustums (cut-off pyramids or cones)
Cylinders, cones, spheres
Different types of wedges

Later Chinese mathematicians like Shen Kuo and Yang Hui continued to advance geometry.

Islamic Golden Age

During the Islamic Golden Age, mathematicians also made big strides in geometry. Thābit ibn Qurra provided new proofs for the Pythagorean theorem that worked for all triangles, not just special ones.

Some recent studies suggest that girih tiles, used in Islamic art, have complex geometric properties. They might even be related to modern ideas like fractals.

Renaissance

An old drawing by Albrecht Dürer showing a scholar with a compass, a tool important in geometry and art.

During the Renaissance (14th to 16th centuries), Greek geometry ideas came back to Europe, often through Arabic writings. People started to learn Euclid's methods again. This led to many new geometry ideas.

Artists in the Renaissance made big advances in perspective drawing. This was a new way to show depth and distance in paintings. Filippo Brunelleschi showed how to use geometry to create realistic perspective. Soon, many artists like Leonardo da Vinci used these techniques.

Leon Battista Alberti wrote a book, De pictura, explaining the math behind perspective using Euclidean geometry. Later, Piero della Francesca expanded on this, showing how to draw 3D shapes in perspective. These ideas spread across Europe and changed art forever.

Modern Geometry

The 17th Century

The 17th century brought two major changes to geometry. The first was analytic geometry, created by René Descartes and Pierre de Fermat. This linked geometry with coordinates and equations. It was a key step for developing calculus and modern physics.

The second was the study of projective geometry by Girard Desargues. This type of geometry looks at how points and lines relate to each other without caring about measurements.

Later in the 17th century, Isaac Newton and Gottfried Wilhelm Leibniz independently developed calculus. While not geometry itself, calculus became a powerful tool for solving geometry problems, like finding tangent lines to curves or areas enclosed by them.

The 18th and 19th Centuries

Non-Euclidean Geometry

For a long time, mathematicians tried to prove Euclid's Fifth Postulate (the parallel postulate) from his other four rules. But they always failed. Around the early 1800s, mathematicians like Carl Friedrich Gauss, János Bolyai, and Nikolai Lobachevsky had a new idea. They wondered what would happen if the parallel postulate was false.

They successfully created new types of geometry where this postulate was not true. These are called non-Euclidean geometries. In 1854, Bernhard Riemann used calculus to study the geometry of curved surfaces, leading to another non-Euclidean geometry. Riemann's work later became very important for Albert Einstein's theory of relativity.

It was later proven that these non-Euclidean geometries were just as logically sound as Euclidean geometry. This showed that geometry wasn't just about our physical space. It could be about different kinds of spaces.

New Rules for Geometry

The work on the parallel postulate showed that mathematicians needed to be very careful with their logic. Euclid's original rules had some small gaps. So, in 1894, David Hilbert created a new, complete set of rules for geometry, called Hilbert's axioms. These rules made sure that geometry relied only on pure logic, not on drawings or intuition.

Geometry in More Dimensions

The 19th century also saw the idea of Euclidean space being extended beyond three dimensions. Ludwig Schläfli explored shapes in four or more dimensions. He found that there are special regular shapes in four dimensions, similar to the Platonic solids in three dimensions.

William Kingdon Clifford introduced geometric algebra in 1878. This system helps describe how geometric objects can be moved, rotated, or reflected in space, especially in four dimensions.

The 20th Century

In the 20th century, algebraic geometry grew. It studied curves and surfaces using algebra. Finite geometry, which studies spaces with only a limited number of points, found uses in areas like coding theory and cryptography.

With the rise of computers, new fields like computational geometry and digital geometry appeared. These fields deal with how computers can work with geometric data and algorithms.

Images for kids

Part of the "Tab.Geometry." (Table of Geometry) from the 1728 Cyclopaedia.
Rigveda manuscript in Devanagari.
Pythagorean theorem: a² + b² = c²
Statue of Euclid in the Oxford University Museum of Natural History.
Woman teaching geometry. Illustration at the beginning of a medieval translation of Euclid's Elements, (c. 1310)
Geometry was connected to the divine for most medieval scholars. The compass in this 13th-century manuscript is a symbol of God's act of Creation.
Page from the Al-Jabr wa-al-Muqabilah
An engraving by Albrecht Dürer featuring Mashallah, from the title page of the De scientia motus orbis (Latin version with engraving, 1504).
Discourse on Method by René Descartes