History of calculus facts for kids
Calculus, also known as infinitesimal calculus, is a branch of mathematics that helps us understand how things change. It looks at ideas like limits, continuity, derivatives (how fast something changes), integrals (adding up tiny pieces), and infinite series (sums of endless numbers).
Many of the ideas behind calculus first appeared in ancient Greece, then in China, the Middle East, and later in Europe and India. But the modern form of calculus was developed in the late 1600s by two brilliant minds: Isaac Newton and Gottfried Wilhelm Leibniz. They worked on it separately, which led to a big argument about who invented it first. This argument, called the Leibniz–Newton calculus controversy, lasted until Leibniz died in 1716. Since then, calculus has continued to grow and is used in many areas of science.
Contents
What Does "Calculus" Mean?
In math classes, "calculus" usually means the study of functions and limits. The word "calculus" comes from Latin and means "small pebble." Imagine using little stones for counting distances, votes, or doing math on an abacus. Because of this, the word came to mean a way of calculating things. People were using the word "calculus" in English as early as 1672, even before Newton and Leibniz published their work.
Besides the main types of calculus (differential and integral), the term "calculus" is also used for other specific ways of calculating. For example, there's "propositional calculus" in logic or "process calculus" in computer science.
Early Ideas of Calculus
Ancient Times
Some early ideas that led to integral calculus appeared long ago, but they weren't organized into a clear system.
Egypt and Babylonia
Ancient Egyptians, around 1820 BC, had ways to calculate volumes and areas, which is a goal of integral calculus. These formulas were for specific numbers and weren't always perfectly accurate. The Babylonians might have used a method similar to the trapezoidal rule when watching the planet Jupiter.
Greece
In ancient Greece, Eudoxus of Cnidus (around 408–355 BC) used the "method of exhaustion." This method is a bit like the idea of a limit we use today. He used it to calculate areas and volumes. Later, Archimedes (around 287–212 BC) took this idea even further. He even invented ways of thinking that are similar to modern integral calculus.
Greek mathematicians also thought about "infinitesimals," which are incredibly tiny amounts. Democritus was one of the first to think about dividing objects into an infinite number of slices. But he couldn't quite make sense of how these tiny slices would create a smooth shape like a cone. Around the same time, Zeno of Elea created his famous paradoxes, which made people doubt the idea of infinitesimals.
Archimedes also found a way to draw a tangent line to a curve (other than a circle). This was similar to how we use differential calculus today. He did this by breaking down a point's movement into two parts and then adding them together.
China
The "method of exhaustion" was also developed independently in China by Liu Hui in the 4th century AD to find the area of a circle. In the 5th century, Zu Chongzhi used a method similar to Cavalieri's principle to find the volume of a sphere.
Medieval Times
Middle East
In the Middle East, Ibn al-Haytham (also known as Alhazen, around 965–1040 CE) found a formula for adding up numbers raised to the fourth power. He used this to do something like an integration to calculate the volume of a paraboloid (a 3D shape like a bowl). Some historians believe that the 12th-century mathematician Sharaf al-Dīn al-Tūsī might have used ideas similar to derivatives for cubic equations, but this is still debated.
India
There's evidence that Bhāskara II in India had some early ideas about differential calculus. He even suggested that the "differential coefficient" (similar to a derivative) becomes zero at the highest or lowest point of a function. This shows he understood the idea of infinitesimals. His work also contains an early form of Rolle's theorem. While he didn't fully develop the idea of a derivative, his work showed some important steps.
Later, the Kerala school of astronomy and mathematics in India, especially Madhava of Sangamagrama in the 14th century, explored parts of calculus like Taylor series and infinite series. However, they didn't connect all these different ideas into the two main parts of calculus (derivatives and integrals) or show how they relate to each other, like Newton and Leibniz did later.
Europe
In the 14th century, mathematicians in Europe, like the Oxford Calculators and Nicole Oresme, started studying continuity again. They proved the "Merton mean speed theorem," which describes how a body moving at a steady acceleration covers the same distance as a body moving at a constant speed that is half of the accelerated body's final speed.
Modern Steps Towards Calculus
Integrals
Johannes Kepler's book Stereometrica Doliorum (1615) laid some groundwork for integral calculus. He found a way to calculate the area of an ellipse by adding up the lengths of many lines drawn from a central point.
A big step came in 1635 with Bonaventura Cavalieri's work on his "method of indivisibles." He suggested that volumes and areas could be found by adding up the volumes and areas of extremely thin slices. He found a formula for the area under curves like xn. This was similar to what Archimedes had done for parabolas, but Archimedes' work was lost for a long time. Cavalieri's ideas weren't immediately accepted because they sometimes led to errors, and the idea of infinitesimals was still new and confusing.
Later, Evangelista Torricelli expanded Cavalieri's work to other curves. John Wallis then generalized the formula to include fractional and negative powers in 1656. In 1659, Pierre de Fermat came up with a clever way to calculate the integral of any power function directly.
Derivatives
In the 1600s, European mathematicians like Isaac Barrow, René Descartes, Pierre de Fermat, Blaise Pascal, and John Wallis talked about the idea of a derivative. Fermat, in particular, introduced the idea of "adequality" around 1636. This was a way to think about equality with a tiny, tiny error term. This method helped find the highest and lowest points of curves and draw tangent lines, which is very close to what differentiation does.
Isaac Newton later said that his own early ideas about calculus came directly from "Fermat's way of drawing tangents."
The Fundamental Theorem of Calculus
The formal study of calculus brought together Cavalieri's infinitesimals with the "calculus of finite differences" (which looks at how things change in steps) and Fermat's adequality. John Wallis, Isaac Barrow, and James Gregory combined these ideas. Barrow and Gregory, around 1670, proved early versions of the second fundamental theorem of calculus. This theorem shows that integrals can be found using a function's antiderivatives (the opposite of a derivative).
The first complete proof of the fundamental theorem of calculus was given by Isaac Barrow.
Other Important Ideas
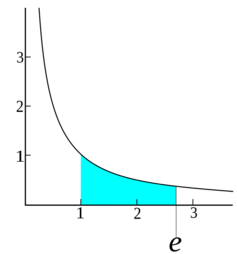
One important step for calculus was finding a way to calculate the "antiderivative" for the function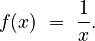 
This is like finding the area under the curve of a rectangular hyperbola. In 1647, Gregoire de Saint-Vincent noticed that the function for this area had a special property: 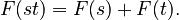Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): F(st) = F(s) + F(t) . This meant that multiplying numbers turned into adding them, just like with logarithms. So, this function was first called the "hyperbolic logarithm." Later, after Leonhard Euler explored the special number 'e' (about 2.71828...), this function became known as the natural logarithm, which has the property that its derivative is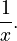 Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{1}{x} .
The first proof of Rolle's theorem was given by Michel Rolle in 1691. The modern "mean value theorem" was stated by Bernard Bolzano and Augustin-Louis Cauchy much later. Many others, like Isaac Barrow and Christiaan Huygens, also made important contributions.
Newton and Leibniz: The Founders
Before Newton and Leibniz, the word "calculus" just meant any kind of math. But after their work, it became the name for this new field of mathematics based on their amazing ideas. Newton and Leibniz, building on earlier work, independently created the main ideas of infinitesimal calculus in the late 1600s. Leibniz did a lot to create clear and useful ways to write down calculus (notation). Newton, on the other hand, found some of the most important ways to use calculus in physics, especially with integral calculus.
By the mid-1600s, European mathematicians were looking more at new ideas rather than just old Greek math.
Newton came to calculus while studying physics and geometry. He saw calculus as a way to describe motion and how things change in size. Leibniz, however, focused on the problem of finding tangent lines and thought of calculus as a deeper explanation of change itself. The most important thing they both realized was the inverse relationship between the integral and the differential of a function (how they are opposites). Others had hinted at this, but Newton and Leibniz were the first to build a whole new system of math around it, with new words and symbols.
Newton's Approach
Newton didn't publish one big book explaining his calculus right away. Many of his math discoveries were shared through letters or were hidden within his other famous works, like Principia (about gravity and motion) and Opticks (about light). Newton started his math training at Cambridge under Isaac Barrow. He quickly showed his talent and learned the latest theories. By 1664, he made a big contribution by improving the binomial theorem, which helps expand expressions like (a+b)n. Newton showed that this theorem could be used with infinite series (sums that go on forever). He was okay with thinking of infinite series not just as approximations, but as different ways to write numbers.
Many of Newton's most important ideas came to him during the plague years of 1665–1666. He later called this time "the prime of my age for invention." During his isolation, he wrote down his first ideas about "fluxionary calculus" in an unpublished paper called De Analysi per Aequationes Numero Terminorum Infinitas. In this paper, Newton found the area under a curve by first looking at a tiny, momentary rate of change, and then figuring out the total area. He imagined a very small triangle whose area depended on 'x' and 'y'. He then thought about a tiny increase in 'x', calling it 'o' (a letter, not the number zero). He recalculated the area using the binomial theorem, removed all terms with 'o', and got a new expression for the area. Importantly, Newton would then "blot out" the terms with 'o' because they would be "nothing in respect to the rest" when 'o' became infinitely small.
At this point, Newton started to understand the main idea of inversion (that derivatives and integrals are opposites). He had found an expression for the area under a curve by looking at a tiny increase at a point. The fundamental theorem of calculus was built into his calculations. Even though his new ideas were powerful, Newton knew they had logical weaknesses. He admitted that "errors are not to be disregarded in mathematics, no matter how small."
To make calculus more precise, Newton wrote Methodus Fluxionum et Serierum Infinitarum in 1671. In this book, Newton's focus on what could be observed and measured shaped his fluxional calculus. He used ideas of instantaneous motion and infinitesimals in a less formal way. He used math as a tool to explain the physical world. Newton's revised calculus was based on the idea of continuity; he redefined his calculations in terms of continuous, flowing motion. For Newton, changing amounts weren't made of tiny, separate pieces, but were created by the undeniable fact of motion. Like many of his works, Newton delayed publishing this book until 1736.
Newton tried to avoid using infinitesimals directly by making calculations based on ratios of changes. In Methodus Fluxionum, he called the rate of change a "fluxion" (represented by a dotted letter, like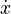 
for a changing quantity 
). The changing quantity itself he called a "fluent." This calculus of ratios continued to develop and was clearly explained in his 1676 text De Quadratura Curvarum. Here, Newton defined what we now call the derivative as the "ultimate ratio of change"—the ratio between tiny, disappearing increases, at the exact moment they vanish. He explained this by thinking about motion:
"For by the ultimate velocity is meant that, with which the body is moved, neither before it arrives at its last place, when the motion ceases nor after but at the very instant when it arrives... the ultimate ratio of evanescent quantities is to be understood, the ratio of quantities not before they vanish, not after, but with which they vanish."
Newton developed his fluxional calculus to avoid the informal use of infinitesimals in his calculations.
Leibniz's Approach
While Newton started his calculus in 1665–1666, his discoveries weren't widely known until later. During that time, Leibniz also worked to create his own calculus. Unlike Newton, who started math young, Leibniz began his serious math studies when he was older and already very smart. He was a polymath, meaning he was an expert in many fields, including metaphysics (the study of reality), law, economics, politics, and logic. To understand Leibniz's thinking in calculus, it helps to remember his background, especially his idea of the universe as made of tiny, simple units called "monads," and his goal of creating a precise logical system where "all truths of reason would be reduced to a kind of calculation."
In 1672, Leibniz met the mathematician Christiaan Huygens, who encouraged him to spend more time on math. By 1673, he was reading Blaise Pascal's Traité des Sinus du Quarte Cercle (Treatise on the Sines of the Quadrant of a Circle). It was during his self-taught research that Leibniz said "a light turned on." Like Newton, Leibniz saw the tangent line as a ratio, but he described it simply as the ratio between the 'y' values (ordinates) and 'x' values (abscissas). He continued this idea to argue that the integral was actually the sum of the 'y' values for tiny, tiny intervals in 'x' – in other words, the sum of an infinite number of very thin rectangles. From these definitions, the inverse relationship (or differential) became clear, and Leibniz quickly saw the potential to create a whole new system of mathematics. While Newton used several approaches, Leibniz made infinitesimals the core of his notation and calculus.
In his notes from October-November 1675, Leibniz wrote down his discoveries and tried out different ways to write them. He was very careful about the symbols he used, showing his earlier goal of creating a precise logical symbolism. Eventually, Leibniz used dx and dy for the tiny increases in 'x' and 'y', and a long s (∫) for the sum of infinitely many tiny rectangles. This became the integral symbol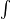 
we use today.
While modern math uses Leibniz's notation, his logical foundation was different from ours. Leibniz fully accepted infinitesimals and wrote a lot about them, wanting "not to make of the infinitely small a mystery, as had Pascal." For Leibniz, infinitesimals were "less than any given quantity." He believed the world was made of infinitesimal points, and he wasn't bothered by the lack of scientific proof for their existence. For Leibniz, the idea of continuity (things changing smoothly) proved that his calculus was valid. Three hundred years after Leibniz's work, Abraham Robinson showed that using infinitesimal quantities in calculus could be given a strong mathematical foundation.
Their Legacy
The creation of calculus was a unique moment in mathematics. Calculus is the math of motion and change, and inventing it required a whole new mathematical system. It's important to remember that Newton and Leibniz didn't create the exact same calculus, and they didn't think of it exactly as we do today. While both worked on creating a math system for changing quantities, their basic ideas were different. For Newton, change was about how a quantity varied over time. For Leibniz, it was about the difference between infinitely close values. The words they used to describe change were also different.
Historically, there was a big debate about who "invented" calculus first. This argument, called the Leibniz and Newton calculus controversy, involved Leibniz (who was German) and Newton (who was English). It caused a split in the European math community that lasted over a century. Leibniz was the first to publish his work, but it's clear that Newton had started his work several years before Leibniz and had already developed a theory of tangents.
It's not known how much Leibniz might have been influenced by Newton's earlier work. The first accusations of plagiarism were made by students and supporters of the two scientists, but after 1711, both Newton and Leibniz got personally involved.
This argument caused English-speaking mathematicians to be separated from those in continental Europe for many years. It wasn't until the 1820s that Leibniz's analytical calculus became accepted in England, thanks to the efforts of the Analytical Society. Today, both Newton and Leibniz are recognized for independently developing the basic ideas of calculus. However, it was Leibniz who gave the new field the name we use today: "calculus." Newton called his system "the science of fluents and fluxions."
The work of both Newton and Leibniz is still seen in the notation we use today. Newton introduced the notation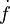 
for the derivative of a function f. Leibniz introduced the symbol 
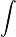for the integral and wrote the derivative of a function y with respect to x as 
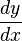. Both of these are still used.
Since Newton and Leibniz, many mathematicians have helped develop calculus further. One of the first and most complete books on both infinitesimal and integral calculus was written in 1748 by Maria Gaetana Agnesi.
Later Developments
Calculus of Variations
The calculus of variations started with a problem from Johann Bernoulli in 1696. Leonhard Euler was the first to really develop this subject, starting in 1733, and he gave it its name. Joseph Louis Lagrange also made many contributions. Many other mathematicians, like Carl Friedrich Gauss and Karl Weierstrass, helped make this area of calculus more rigorous and solid.
Operational Methods
Antoine Arbogast (1800) was the first to separate the symbol for an operation (like taking a derivative) from the quantity it acts on in a differential equation. Francois-Joseph Servois (1814) gave correct rules for this. Later, George Boole used these methods a lot, and Hermann Grassmann and Hermann Hankel also made great use of this theory.
Integrals
Niels Henrik Abel was one of the first to think about which differential equations could be solved using normal functions. Augustin Louis Cauchy worked on the general theory of finding definite integrals, and this topic was very important in the 19th century. Many mathematicians, including Adrien-Marie Legendre, Siméon Denis Poisson, and Leopold Kronecker, made important contributions.
Leonhard Euler first studied what are now called "Eulerian integrals." These include integrals like: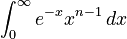 
If n is a positive integer, this integral equals 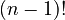Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): (n-1)! (n-1 factorial). But it also works for other positive numbers and defines a special function called the gamma function, which is given the symbol 
.
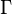How Calculus is Used
Calculus was used in physics and astronomy right from the start. Throughout the 1700s, these uses grew, until by the end of the century, scientists like Pierre-Simon Laplace and Joseph Louis Lagrange were using calculus to understand almost all forces. Lagrange (1773) introduced the idea of "potential" into dynamics, which was further developed by Green (1827) and Carl Friedrich Gauss (1840). Many other famous scientists, including Bernhard Riemann and John von Neumann, contributed to this area.
It's hard to list all the ways calculus is used in physical problems. Some examples include:
- Euler's work on vibrating strings.
- Sophie Germain's studies on elastic membranes.
- Jean Baptiste Joseph Fourier's work on how heat spreads.
- Augustin-Jean Fresnel's theories on light.
- James Clerk Maxwell, Hermann von Helmholtz, and Heinrich Rudolf Hertz's work on electricity.
- Lord Rayleigh's studies on acoustics (sound).
Calculus has also been introduced into the social sciences, starting with Neoclassical economics. Today, it's a very important tool in modern economics.
Images for kids
-
Archimedes used the method of exhaustion to calculate the area under a parabola in his work Quadrature of the Parabola.
See also
- Analytic geometry
- History of logarithms
- History of mathematics
- Non-standard calculus
