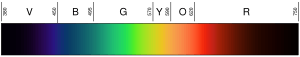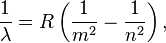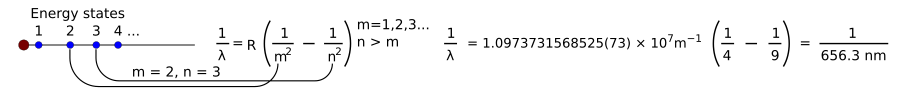Quantum mechanics facts for kids
Quantum mechanics (often called QM) is a branch of physics. It helps us understand how the tiniest things in the universe work. This includes the super-small parts that make up atoms, like protons, neutrons, and electrons.
QM also explains how waves of energy like light behave. It uses special mathematics to describe these tiny particles and waves. This is because they act in very strange ways that are different from what we see in our everyday lives. Quantum mechanics is super important for understanding both physics and chemistry.
The word quantum comes from Latin and means 'how much'. So, a quantum of energy is a specific, tiny amount of energy. Light sources, like candles or lasers, send out light in tiny packets called photons. Each photon is like a small package carrying a certain amount of energy.
Contents
Waves and Light Particles
Photons are particles much smaller than atoms. The more photons a lamp sends out, the brighter the light appears. Light is a type of energy that acts like waves in water or radio waves.
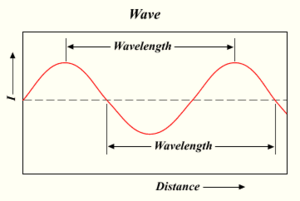
The distance from the top of one wave to the top of the next is called its 'wavelength'. Each photon carries a certain amount of energy. This energy depends on its wavelength.
A light's color depends on its wavelength. For example, violet light (like in a rainbow) has a wavelength of about 400 nanometers (nm). This is a very tiny measurement. Photons with wavelengths from 10 to 400 nm are called ultraviolet (UV) light. Our eyes cannot see UV light.
On the other side, red light has a wavelength of about 700 nm. Infrared light has even longer wavelengths, from about 700 nm up to 300,000 nm. We cannot see infrared light either.
Wavelengths are not always so small. Radio waves have much longer wavelengths. For instance, the waves for your FM radio can be several meters long. Each photon has a specific amount of energy linked to its wavelength. The shorter a photon's wavelength, the more energy it has. So, an ultraviolet photon has more energy than an infrared photon.
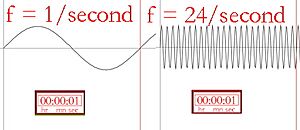
Wavelength and frequency (how many wave tops pass by per second) are connected. A longer wavelength means a lower frequency, and a shorter wavelength means a higher frequency.
If light is infrared (lower frequency than red light), each photon can heat up what it touches. This is why a strong infrared lamp (a heat lamp) makes you feel warm. It's because of the energy in those many photons.
Humans cannot see infrared light. But we can feel its heat. For example, if you walk past a brick building heated by the sun, you feel warmth from it without touching it.
If light is ultraviolet (higher frequency than violet light), each photon has a lot of energy. Enough energy to hurt skin cells and cause a sunburn. Most sunburns are not caused by heat. They are caused by the high energy of the sun's UV rays damaging your skin.
Even higher frequencies of light can go deeper into the body. X-rays and gamma rays have so much energy they can kill cells. Humans cannot see or feel ultraviolet light, X-rays, or gamma rays. We only know we've been exposed when we get a radiation burn.
Places where it's important to kill germs often use ultraviolet lamps. These lamps destroy bacteria and fungi. X-rays and gamma rays are sometimes used to kill cancer cells.
Quantum mechanics began when scientists found that a certain frequency of light always means a certain amount of energy. This means energy is directly related to frequency (E ∝ f). The higher the frequency, the more energy a photon has, and the more damage it can do. Later, quantum mechanics grew to explain the inside structure of atoms. It also explains how a photon can interfere with itself, and many other things never imagined in classical physics.
Quantization: Energy in Steps
Max Planck discovered the link between frequency and energy. Before him, no one thought frequency would be directly linked to energy. This means if one doubles, the other doubles too.
Planck figured out a formula:
- E = h × f
This means energy equals h times frequency. The h is a special number called Planck's constant. It's named after him.
Quantum mechanics is based on this idea. A photon of a certain frequency always has a certain amount of energy. Also, a specific kind of atom can only give off certain frequencies of light. This means it can only give off photons with certain amounts of energy.
History of Quantum Mechanics
Long ago, Isaac Newton thought light was made of tiny particles. Christiaan Huygens thought light was made of waves. Scientists believed something couldn't be both a particle and a wave at the same time.
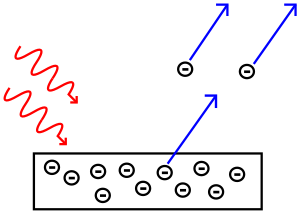
But experiments showed both ideas were right! Light acts like both waves and particles. An experiment by Thomas Young showed light acts like a wave. The Photoelectric effect, discovered by Albert Einstein, proved light acts like particles carrying specific amounts of energy. This strange behavior is called "wave-particle duality". Later, physicists found that everything, not just light, behaves like both a wave and a particle. This effect is just much smaller for big objects.
Many brilliant people helped discover the basic ideas of quantum mechanics. Some of them are Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, and Richard Feynman. They did their work in the first half of the 20th century.
Beyond Planck's Discoveries
Early quantum mechanics ideas were made to explain the light from glowing hydrogen. The quantum theory of the atom also had to explain why electrons stay in their orbits. Older ideas couldn't explain this. They predicted electrons would lose energy and fall into the atom's center.
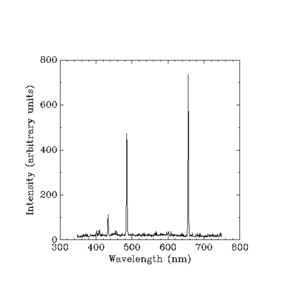
Hydrogen lamps work like neon lights. But each element, like hydrogen or neon, gives off its own unique set of light colors (and frequencies). Scientists learned they could identify elements by the light they produce. But they couldn't figure out *how* these specific frequencies were determined.
Then, a Swiss mathematician named Johann Jakob Balmer found an equation for hydrogen's visible light:
Here, B is a number Balmer found to be 364.56 nm.
Later, the equation was made more general:
Here, R is the Rydberg constant, and n must be greater than m. This equation can predict frequencies for many types of light (ultraviolet, visible, and infrared).
In 1905, Albert Einstein used Planck's idea. He showed that a beam of light is made of photons. The energy of each photon depends on its frequency. Einstein's idea started the concept in quantum mechanics that all tiny particles, like electrons, protons, and neutrons, are both waves and particles at the same time. This is called wave-particle duality.
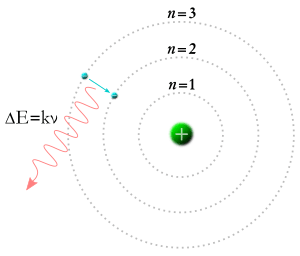
In 1913, Niels Bohr had a new idea. He suggested that electrons could only exist in certain orbits around an atom's nucleus. The numbers m and n in the equation above could represent these orbits.
If a photon hits an electron, the electron absorbs its energy and moves to a higher orbit. If an electron falls from a higher orbit to a lower one, it gives off energy as a photon. The photon's energy equals the energy difference between the two orbits. This energy then determines the photon's frequency and color.
Everything seemed to fit well. But one big question remained: Why do the specific colors of light from glowing hydrogen (or any other element) have different brightness levels? And why are these brightness differences always the same for each element?
Werner Heisenberg took on the challenge of explaining the brightness, or "intensity," of each light line. He couldn't use a simple rule like Balmer's. He had to use complex math from classical physics. This math involved things like the mass and charge of an electron.
Classical physics already had answers for the brightness of light bands. But it predicted a continuous rainbow, not separate color bands. Heisenberg's explanation was that there's a law that predicts specific frequencies of light. These frequencies are spaced out when electrons move between orbits close to the nucleus. But they get closer together as electrons move between farther orbits.
Heisenberg found a way to predict these intensities. His work led to a new way of doing physics.
Further Mysteries
In the early days of quantum mechanics, Albert Einstein thought that if QM was right, it would mean "spooky action at a distance." It turned out that QM was right, and this "spooky connection" actually happens. This is now called "quantum entanglement".
When two things (like photons or electrons) interact, they share a common description in quantum mechanics. When they are separated, they keep this shared description. For example, two entangled electrons might both have "up" and "down" spin at the same time. If you measure one electron and find it has "up" spin, the other electron, no matter how far away, will instantly have "down" spin when measured.
Einstein argued this was crazy. He thought the electrons must have had their spins decided all along. He believed quantum mechanics was incomplete because it couldn't predict which spin each electron had. However, later experiments showed that Einstein was wrong.
Heisenberg Uncertainty Principle
In 1925, Werner Heisenberg described the Uncertainty principle. It says that the more precisely we know where a particle is, the less precisely we can know how fast it's going and in what direction. And vice versa. Physicists often talk about momentum instead of speed. Momentum is an object's speed in a certain direction multiplied by its mass.
The reason for Heisenberg's uncertainty principle is that we can never know both the exact location and the exact momentum of a particle at the same time. To measure a particle, we often use light. If we use a high-energy light beam, we can pinpoint its location. But the high-energy photon transfers energy to the particle, changing its speed. If we use a low-energy photon, we can know its speed better. But the longer wavelength of the light means we can't pinpoint its exact location.
This principle means there are many pairs of measurements for which we can't know both precisely about any particle. The more we learn about one, the less we can know about the other.
Even Albert Einstein had trouble accepting this strange idea. He famously said, "God does not play dice." To this, Danish physicist Niels Bohr replied, "Einstein, don't tell God what to do."
Uses of Quantum Mechanics
Electrons surround every atom's nucleus. Chemical bonds link atoms to form molecules. A chemical bond forms when electrons are shared between atoms. So, QM is the physics behind chemical bonds and all of chemistry. QM helps us understand how molecules are made and what their properties are.
QM can also help us understand huge things, like stars and even the whole universe. QM is a very important part of the theory of how the universe began, called the Big Bang.
Everything made of matter is pulled towards other matter by a force called gravity. Einstein's theory of gravity is called general relativity. A challenge in modern physics is that some ideas from QM don't seem to agree with general relativity. Scientists are still working on this!
QM explains why all electronic technology works. This means QM explains how computers work, since they are electronic machines. Early computer designers in the 1950s and 60s didn't need to think about QM. But designing today's powerful integrated circuits and computer memory needs QM.
QM has also made possible technologies such as:
- Spectroscopy (studying how light interacts with matter)
- Lasers
- MRIs (medical scans)
- CDs and DVDs
Why Quantum Mechanics is Hard to Learn
QM is a challenging subject for a few reasons:
- QM explains things in very different ways from what we learn about the world every day.
- Understanding QM needs more advanced mathematics than just algebra. It uses matrix algebra, complex numbers, and probability theory.
- Even physicists are not completely sure what some QM equations tell us about the real world.
- QM suggests that atoms and tiny particles behave in strange ways. These ways are completely unlike anything we see in our daily lives.
- QM describes things that are extremely small. We cannot see some of them without special equipment, and many we cannot see at all.
QM describes nature in a way that is different from how we usually think about science. It tells us how likely some things are to happen, instead of telling us they certainly will happen.
One strange idea from QM is the "Schrödinger's cat" effect. It suggests that certain properties of a particle, like its position or "spin", cannot be known until something measures them. Before the measurement, the particle is in a "superposition of states." This means its properties have many values at the same time. Schrödinger used the example of a cat in a box to show how weird this is. He said that if a cat's life or death depended on a quantum event, then before anyone looked, the cat would be "mixed or smeared out in equal parts" – both alive and dead at the same time!
Reduced Planck's Constant
People often use the symbol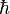 
, which is called "h-bar." It's equal to 
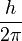. H-bar is a unit of angular momentum. When this unit is used to describe the orbits of electrons in atoms, the angular momentum of any electron in orbit is always a whole number.
Images for kids
-
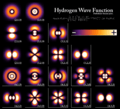
Wave functions of the electron in a hydrogen atom at different energy levels. Quantum mechanics cannot predict the exact location of a particle in space, only the probability of finding it at different locations. The brighter areas represent a higher probability of finding the electron.
-
Fig. 1: Probability densities corresponding to the wave functions of an electron in a hydrogen atom possessing definite energy levels (increasing from the top of the image to the bottom: n = 1, 2, 3, ...) and angular momenta (increasing across from left to right: s, p, d, ...). Denser areas correspond to higher probability density in a position measurement. Such wave functions are directly comparable to Chladni's figures of acoustic modes of vibration in classical physics and are modes of oscillation as well, possessing a sharp energy and thus, a definite frequency. The angular momentum and energy are quantized and take only discrete values like those shown (as is the case for resonant frequencies in acoustics)
-
Position space probability density of a Gaussian wave packet moving in one dimension in free space.
-
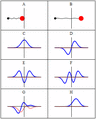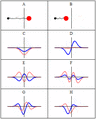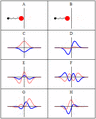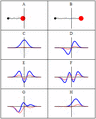
Some trajectories of a harmonic oscillator (i.e. a ball attached to a spring) in classical mechanics (A-B) and quantum mechanics (C-H). In quantum mechanics, the position of the ball is represented by a wave (called the wave function), with the real part shown in blue and the imaginary part shown in red. Some of the trajectories (such as C, D, E, and F) are standing waves (or "stationary states"). Each standing-wave frequency is proportional to a possible energy level of the oscillator. This "energy quantization" does not occur in classical physics, where the oscillator can have any energy.
-
Max Planck is considered the father of the quantum theory.
-
The 1927 Solvay Conference in Brussels was the fifth world physics conference.
.jpg)
See also
In Spanish: Mecánica cuántica para niños
