Mathematics facts for kids
Mathematics is the study of numbers, shapes, and patterns. The word comes from the Greek word "máthema," which means "science, knowledge, or learning." People sometimes shorten it to maths in places like England and Australia. In the United States and Canada, it's often called math. These shorter words are often used for subjects like arithmetic, geometry, or simple algebra that students learn in school.
Mathematics helps us understand:
- Numbers: How we count things.
- Structure: How things are organized. This part is often called algebra.
- Place: Where things are and how they are arranged. This is usually called geometry.
- Change: How things become different over time. This is known as analysis.
Mathematics is very useful for solving problems in the real world. Many people, not just mathematicians, use math every day. Jobs in business, science, engineering, and construction all need some math skills.
Contents
Solving Problems with Math
Mathematics solves problems using logic. One main tool mathematicians use is deduction. Deduction is a special way of thinking. It helps us discover and prove new truths using things we already know are true.
For a mathematician, knowing why something is true (called a proof) is as important as knowing that it is true. This "why" is often found using deduction. This is what makes math thinking different from other sciences. Other sciences might use experiments or interviews to find answers.
Mathematicians use logic and reasoning to create general rules. These rules are a big part of mathematics. They leave out unimportant details so that one rule can work for many situations. By finding general rules, math can solve many problems at once. These rules can be called theorems if they have been proven true. If we don't know if they are true yet, they are called conjectures.
Sometimes, math explores ideas and rules that we don't fully understand yet. Often, ideas in math are chosen because they seem simple or elegant. Interestingly, some of these ideas, first studied in math, are later found to exist in the real world. Learning about math rules and ideas helps us understand the world better. Some basic math problems include addition, subtraction, multiplication, and division. Algebra problems involve finding the value of certain variables. A calculator can help solve many math problems quickly.
Main Areas of Math Study
Understanding Numbers
Mathematics involves studying numbers and how much of something there is. Many math fields, like set theory and mathematical logic, look at numbers. Number theory mainly focuses on how whole numbers work, rather than just what numbers are.
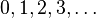 |
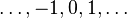 |
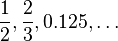 |
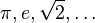 |
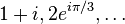 |
| Natural numbers | Integers | Rational numbers | Real numbers | Complex numbers |
 |
 |
 |
 |
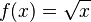 |
| Ordinal numbers | Cardinal numbers | Math operations | Math relationships | Functions |
Studying Structure
Many parts of mathematics look at the structure of objects. Most of these areas are part of algebra.
 |
 |
 |
 |
|
| Number theory | Abstract algebra | Linear algebra | Order theory | Graph theory |
Exploring Shapes
Some areas of mathematics study the shapes of things. Most of these are part of geometry.
 |
 |
 |
 |
|
| Topology | Geometry | Trigonometry | Differential geometry | Fractal geometry |
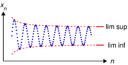
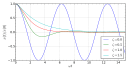
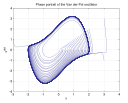
Looking at Change
Some parts of mathematics study how things change. Most of these are part of analysis.
 |
 |
 |
| Calculus | Vector calculus | Analysis |
 |
 |
 |
| Differential equations | Dynamical systems | Chaos theory |
Applied Mathematics
Applied mathematics uses math to solve problems in other areas. This includes fields like engineering, physics, and computer science.
Some areas of applied mathematics are:
- Numerical analysis
- Optimization
- Probability theory
- Statistics
- Mathematical finance
- Game theory
- Mathematical physics
- Fluid dynamics
- Computational algorithms
Famous Math Ideas
These are some famous theorems and ideas that have interested many people.
- Pythagorean theorem
- Fermat's Last Theorem
- Goldbach's conjecture
- Twin Prime Conjecture
- Gödel's incompleteness theorems
- Poincaré conjecture
- Cantor's diagonal argument
- Four color theorem
- Euler's Identity
These theorems and conjectures have greatly changed mathematics:
- Riemann hypothesis
- Continuum hypothesis
- P Versus NP
- Central limit theorem
- Fundamental theorem of calculus
- Fundamental theorem of algebra
- Fundamental theorem of arithmetic
How Math is Studied
Understanding what mathematics is also changes how mathematicians study it.
- Philosophy of Mathematics
- Foundations of mathematics
- Set theory
- Symbolic logic
- Category theory
- Logic
- Table of mathematical symbols
History of Math and Mathematicians
This section looks at the history of mathematics and the people who study it.
- History of mathematics
- Timeline of mathematics
- Mathematicians
- Fields Medal
- Abel Prize
- Millennium Prize Problems
- International Mathematical Union
- Mathematics competitions
Math Awards
There is no Nobel Prize in mathematics. However, mathematicians can receive the Abel Prize and the Fields Medal for their important work.
The Clay Mathematics Institute has offered one million dollars to anyone who solves one of the Millennium Prize Problems.
Tools for Math
Many tools help us do mathematics or find answers to math problems.
- Older tools
- Abacus
- Napier's bones, slide rule
- Ruler and Compass
- Mental calculation (doing math in your head)
- Newer tools
- Calculators and computers
- Programming languages
- Computer algebra systems
- Internet shorthand notation
- statistics software (like SPSS)
- SAS programming language
- R (programming language)
Related Pages
- List of mathematicians
- Timeline of women in mathematics
- American Mathematical Society
- Society for Industrial and Applied Mathematics
- Mathematics Genealogy Project
Images for kids
-
The Ulam spiral shows how prime numbers are spread out.
-
The numbers used in the Bakhshali manuscript, an old Indian math text.
-
Fibonacci, an Italian mathematician who brought the numbers we use today to the Western world.
-
Leonhard Euler helped create much of the math notation we use now.
-
Carl Friedrich Gauss, often called the "prince of mathematicians."
-
Euler's identity, a famous math formula.
-
The front side of the Fields Medal, a top award in math.
See also
 In Spanish: Matemáticas para niños
In Spanish: Matemáticas para niños









