Timeline of mathematics facts for kids

This is a timeline showing the amazing journey of mathematics through history! It's split into three main parts, based on how people wrote down their math ideas:

• Rhetorical Stage: When people described math using only words.
• Syncopated Stage: When they started using short symbols or abbreviations for numbers and math actions.
• Symbolic Stage: When they developed full systems of symbols to write down complex math formulas, like we do today.

Early Math: The Rhetorical Stage

This was a time when people talked about math using only words, long before we had numbers and symbols like we do now.

Before 1000 BC: Ancient Discoveries

• Around 70,000 BC – In South Africa, early humans made geometric patterns on rocks, showing an early interest in shapes.
• Around 35,000 BC to 20,000 BC – People in Africa and France made the first known attempts to measure time, possibly using tools like the Lebombo bone.
• Around 20,000 BC – In the Nile Valley, the Ishango bone might be one of the earliest signs of understanding prime numbers and a method like Egyptian multiplication.
• Around 3400 BC – In Mesopotamia, the Sumerians created the first number system and ways to measure weights and sizes.
• Around 3100 BC – Ancient Egyptians developed an early decimal system, allowing them to count very large numbers by adding new symbols.
• Around 2800 BC – The Indus Valley Civilisation in India used decimal measurements for weights and sizes, showing great precision.
• 2700 BC – Egyptians were using very precise surveying techniques.
• 2400 BC – Egypt developed a very accurate calendar based on astronomy.
• Around 2000 BC – In Mesopotamia, the Babylonians used a base-60 number system and found an early estimate for π (about 3.125).
• Around 1800 BC – The Plimpton 322 tablet from Babylon shows the oldest known examples of Pythagorean triples (sets of numbers that fit the Pythagorean theorem).
• 1800 BC – The Moscow Mathematical Papyrus from Egypt showed how to find the volume of a frustum (a shape like a cone with its top cut off).
• 1650 BC – The Rhind Mathematical Papyrus from Egypt (a copy of an older text) showed an early value for π (about 3.16), an attempt to square the circle, and ways to solve simple equations.
• The Rhind Mathematical Papyrus also has early examples of combinatorial math, which is about counting arrangements.

Symbols Emerge: The Syncopated Stage

In this stage, people started using abbreviations and early symbols for numbers and common math operations.

1st Millennium BC: New Ways to Write Math

• Around 1000 BC – Egyptians used simple fractions, but mostly unit fractions (like 1/2 or 1/3).
• First half of 1st millennium BC – In India, Yajnavalkya described the movements of the Sun and Moon, creating a 95-year cycle to keep them in sync.
• Around 800 BC – Baudhayana in India wrote about quadratic equations and calculated the square root of two very accurately. He also had an early version of the Pythagorean Theorem.
• Around 8th century BC – The Yajurveda in India introduced the idea of infinity, saying that if you add or remove a part from infinity, it's still infinity.
• 1046 BC to 256 BC – In China, the Zhoubi Suanjing covered arithmetic, geometry, and proofs.
• 624 BC – 546 BC – In Greece, Thales of Miletus is credited with several important geometry theorems.
• Around 600 BC – Other Indian texts called "Sulba Sutras" used Pythagorean triples, showed geometric proofs, and estimated π at about 3.16.
• Second half of 1st millennium BC – The Luoshu Square, a unique magic square, was discovered in China.
• 530 BC – In Greece, Pythagoras studied geometry and music. His group also found out about irrational numbers, like the square root of two.
• Around 500 BC – The Indian grammarian Pānini wrote the Astadhyayi, which used advanced ideas like transformations and recursion, originally for language rules.
• 470 BC – 410 BC – In Greece, Hippocrates of Chios tried to square the circle using shapes called lunes.
• 5th century BC – In India, Apastamba also tried to square the circle and calculated the square root of 2 accurately.
• Around 400 BC – Indian texts like the Surya Prajinapti classified numbers and recognized five different types of infinity.
• 4th century BC – Indian texts used the word "Shunya" for the concept of "void" or zero.
• 4th century BC – China started using Counting rods for calculations.
• 330 BC – In China, the Mo Jing was compiled, an early work on Chinese geometry.
• 300 BC – In India, the Bhagabati Sutra contained early information on combinations.
• 300 BC – In Greece, Euclid wrote his Elements, studying geometry as a system of rules. He proved there are endless prime numbers and showed the Euclidean algorithm.
• Around 300 BC – Brahmi numerals developed in India, which are the ancestors of our modern base 10 number system.
• 300 BC – In Mesopotamia, the Babylonians invented the abacus, an early calculator.
• Around 300 BC – The Indian mathematician Pingala wrote about the first Indian use of zero as a dot and described a binary numeral system. He also showed early signs of Fibonacci numbers and Pascal's triangle.
• 260 BC – In Greece, Archimedes proved that the value of π is between 3 + 1/7 and 3 + 10/71. He also found the area of a circle and estimated the square root of 3 very accurately.
• Around 250 BC – The ancient Olmecs in the New World used a true zero symbol, centuries before it appeared in the Old World.
• 240 BC – In Greece, Eratosthenes created his sieve algorithm to quickly find prime numbers.
• 225 BC – In Greece, Apollonius of Perga wrote On Conic Sections and named the ellipse, parabola, and hyperbola.
• 150 BC – In India, Jain mathematicians wrote the Sthananga Sutra, covering number theory, fractions, equations, and permutations.
• 150 BC – In China, methods like Gaussian elimination, Horner's method, and the use of Negative numbers appeared in The Nine Chapters on the Mathematical Art.
• 190 BC – 120 BC – In Greece, Hipparchus laid the groundwork for trigonometry.
• 50 BC – Indian numerals, which are a descendant of the Brahmi numerals and the first positional notation base-10 number system, began to develop further in India.
• Final centuries BC – The Indian astronomer Lagadha wrote the Vedanga Jyotisha, using geometry and trigonometry for astronomy.

1st Millennium AD: Zero and Algebra Take Shape

• 1st century – In Greece, Heron of Alexandria made a very early, brief mention of square roots of negative numbers.
• Around 2nd century – In Greece, Ptolemy wrote the Almagest, an important astronomy and math book.
• 250 – In Greece, Diophantus used symbols for unknown numbers in his book Arithmetica, which is one of the earliest books on algebra.
• 263 – In China, Liu Hui calculated π using his own special algorithm.
• 300 – The first known use of zero as a decimal digit was introduced by Indian mathematicians.
• Around 340 – In Greece, Pappus of Alexandria stated his hexagon theorem and his centroid theorem.
• Around 400 – The Bakhshali manuscript from India showed an understanding of indices, logarithms to base 2, and calculated square roots very accurately.
• 300 to 500 – The Chinese remainder theorem was developed by Sun Tzu.
• 450 – In China, Zu Chongzhi calculated π to seven decimal places, which was the most accurate calculation for nearly a thousand years.
• 500 – In India, Aryabhata wrote the Aryabhata-Siddhanta, introducing trigonometric functions like sine and cosine and their first tables.
• 6th century – Aryabhata made accurate calculations for astronomical events like eclipses, computed π to four decimal places, and solved linear equations.
• 550 – Hindu mathematicians gave zero a numeral representation in the positional notation Indian numeral system.
• 600 – In China, Liu Zhuo used quadratic interpolation.
• 625 – In China, Wang Xiaotong wrote Jigu Suanjing, solving cubic and quartic equations.
• 7th century – In India, Bhāskara I gave a good approximation of the sine function.
• 7th century – In India, Brahmagupta invented a method for solving certain complex equations and was the first to use algebra for astronomy problems.
• 628 – Brahmagupta wrote the Brahma-sphuta-siddhanta, which clearly explained zero and fully developed the modern place-value Indian numeral system. It also gave rules for working with negative and positive numbers, square roots, and solving equations.
• 721 – In China, Zhang Sui (Yi Xing) computed the first tangent table.
• 8th century – In India, Virasena gave rules for the Fibonacci sequence, explained how to find the volume of a frustum using an infinite process, and understood logarithms to base 2.
• 8th century – In India, Sridhara gave the formula for the volume of a sphere and for solving quadratic equations.
• 773 – In Iraq, Indian math and the Indian numeral system were brought to Baghdad.
• 820 – Al-Khwarizmi, a Persian mathematician, wrote Al-Jabr (where the word Algebra comes from). This book introduced systematic ways to solve linear and quadratic equations. His work also led to the term algorithm.
• Around 850 – In Iraq, al-Kindi was a pioneer in cryptanalysis and frequency analysis (breaking codes).
• Around 850 – In India, Mahāvīra wrote a book with rules for writing fractions as the sum of unit fractions.
• 895 – In Syria, Thābit ibn Qurra worked on cubic equations, generalized the Pythagorean theorem, and found a way to find amicable numbers (pairs of numbers where each is the sum of the other's proper divisors).
• Around 900 – In Egypt, Abu Kamil began to understand the rules of exponents, like .
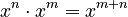• 940 – In Iran, Abu al-Wafa' al-Buzjani extracted roots using the Indian numeral system.
• 953 – Al-Uqlidisi adapted the Hindu–Arabic numeral system for pen and paper, making it easier to use.
• 953 – In Persia, Al-Karaji was the first to separate algebra from geometry, making it more like the algebra we know today. He also discovered the binomial theorem for integer exponents.
• 975 – In Mesopotamia, al-Battani expanded trigonometry to include tangent and secant functions.

Modern Math: The Symbolic Stage

This stage is where math became truly symbolic, with comprehensive systems for writing formulas.

1000–1500: New Ideas and Global Spread

• Around 1000 – Abu Sahl al-Quhi (Kuhi) solved equations higher than the second degree.
• Around 1000 – The Law of sines was discovered by Muslim mathematicians.
• Around 1000 – Pope Sylvester II introduced the abacus using the Hindu–Arabic numeral system to Europe.
• 1000 – Al-Karaji wrote a book with the first known proofs by mathematical induction, proving the binomial theorem and sums of cubes.
• 1070 – Omar Khayyam began classifying cubic equations.
• Around 1100 – Omar Khayyám found general geometric solutions for cubic equations, laying groundwork for analytic geometry. He also extracted roots using the decimal system.
• 12th century – The Arabic numeral system, based on Indian numerals, reached Europe.
• 12th century – Bhaskara Acharya wrote the Lilavati, covering arithmetic, geometry, and equations.
• 12th century – Bhaskara Acharya wrote the Bijaganita (Algebra), which was the first text to recognize that positive numbers have two square roots. He also developed the Chakravala method for solving Pell's equation.
• 12th century – Bhaskara Acharya developed early ideas of differentiation, proved the Pythagorean theorem, and calculated π to 5 decimal places.
• 1130 – Al-Samawal al-Maghribi defined algebra as operating on unknowns using arithmetic tools.
• 1135 – Sharaf al-Din al-Tusi worked on cubic equations, starting the field of algebraic geometry.
• 1202 – Leonardo Fibonacci showed how useful Hindu–Arabic numerals were in his book Liber Abaci.
• 1247 – Qin Jiushao published Shùshū Jiǔzhāng, a math book with many problems solved by polynomial equations.
• 1260 – Al-Farisi gave a new proof for Thabit ibn Qurra's theorem on amicable numbers.
• Around 1250 – Nasir al-Din al-Tusi tried to develop a form of non-Euclidean geometry.
• 1280 – Guo Shoujing and Wang Xun used cubic interpolation for sine calculations.
• 1303 – Zhu Shijie published Precious Mirror of the Four Elements, showing an ancient way to arrange binomial coefficients in a triangle (similar to Pascal's triangle).
• 1356 – Narayana Pandita completed his book Ganita Kaumudi, which included a generalized Fibonacci sequence and an algorithm for generating all permutations.
• 14th century – Madhava discovered the power series expansion for 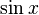, , 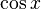and 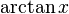, which is now known as the Taylor series.
• 14th century – Parameshvara Nambudiri presented a series form of the sine function and stated the mean value theorem of differential calculus.

15th Century: Expanding Knowledge

• 1400 – Madhava discovered the series expansion for the inverse-tangent function and used it to compute π to 11 decimal places.
• Around 1400 – Jamshid al-Kashi greatly contributed to decimal fractions, using them for approximating numbers like π. He was also the first to use the decimal point notation.
• 15th century – Ibn al-Banna' al-Marrakushi and Abu'l-Hasan ibn Ali al-Qalasadi introduced symbolic notation for algebra.
• 1424 – Ghiyath al-Kashi computed π to sixteen decimal places.
• 1464 – Regiomontanus wrote De Triangulis omnimodus, one of the first texts to treat trigonometry as its own branch of math.
• 1494 – Luca Pacioli wrote Summa de arithmetica, geometria, proportioni et proportionalità, introducing early symbolic algebra.

16th Century: Solving Complex Equations

• 1501 – Nilakantha Somayaji wrote the Tantrasamgraha, covering all 10 cases in spherical trigonometry.
• 1520 – Scipione del Ferro found a way to solve "depressed" cubic equations (cubics without an x² term).
• 1522 – Adam Ries explained the benefits of Arabic digits over Roman numerals.
• 1535 – Nicolo Tartaglia independently developed a method for solving depressed cubic equations.
• 1539 – Gerolamo Cardano learned Tartaglia's method and found a way to solve all cubic equations.
• 1540 – Lodovico Ferrari solved the quartic equation (equations with x⁴).
• 1545 – Gerolamo Cardano came up with the idea of complex numbers.
• 1550 – Jyeṣṭhadeva wrote the Yuktibhāṣā, which proved power series expansions for some trigonometry functions.
• 1572 – Rafael Bombelli used imaginary numbers to solve cubic equations in his Algebra book.
• 1596 – Ludolph van Ceulen computed π to twenty decimal places.

17th Century: Calculus and Probability Begin

• 1614 – John Napier published a table of logarithms.
• 1618 – John Napier made the first references to the mathematical constant e.
• 1619 – René Descartes discovered analytic geometry, which combines algebra and geometry.
• 1629 – Pierre de Fermat developed early ideas of differential calculus.
• 1636 – Muhammad Baqir Yazdi and Descartes jointly discovered a pair of amicable numbers.
• 1637 – Pierre de Fermat claimed to have proven Fermat's Last Theorem.
• 1637 – René Descartes first used the term imaginary number.
• 1654 – Blaise Pascal and Pierre de Fermat created the theory of probability.
• 1665 – Isaac Newton worked on the fundamental theorem of calculus and developed his version of infinitesimal calculus.
• 1671 – James Gregory developed a series expansion for the inverse-tangent function and discovered Taylor's theorem.
• 1673 – Gottfried Leibniz also developed his version of infinitesimal calculus.
• 1675 – Isaac Newton invented an algorithm for finding functional roots (where a function equals zero).
• 1680s – Gottfried Leibniz worked on symbolic logic.
• 1683 – Seki Takakazu discovered the resultant and determinant in algebra.
• 1691 – Gottfried Leibniz discovered how to separate variables for solving differential equations.
• 1693 – Edmund Halley created the first mortality tables, linking death rates to age.
• 1696 – Guillaume de l'Hôpital stated his rule for computing certain limits.
• 1696 – Jakob Bernoulli and Johann Bernoulli solved the brachistochrone problem, an early result in the calculus of variations.

18th Century: New Fields of Math

• 1706 – John Machin developed a fast way to compute π and calculated it to 100 decimal places.
• 1708 – Seki Takakazu discovered Bernoulli numbers.
• 1712 – Brook Taylor developed Taylor series.
• 1722 – Abraham de Moivre stated his formula connecting trigonometric functions and complex numbers.
• 1733 – Abraham de Moivre introduced the normal distribution in probability.
• 1734 – Leonhard Euler introduced the integrating factor technique for solving differential equations.
• 1735 – Leonhard Euler solved the Basel problem, linking an infinite series to π.
• 1736 – Leonhard Euler solved the Seven bridges of Königsberg problem, which helped create graph theory.
• 1742 – Christian Goldbach proposed Goldbach's conjecture, stating that every even number greater than two can be written as the sum of two prime numbers.
• 1747 – Jean le Rond d'Alembert solved the vibrating string problem.
• 1761 – Thomas Bayes proved Bayes' theorem in probability.
• 1761 – Johann Heinrich Lambert proved that π is an irrational number (cannot be written as a simple fraction).
• 1789 – Jurij Vega computed π to 140 decimal places, with 136 correct.
• 1796 – Carl Friedrich Gauss proved that a regular 17-sided polygon can be drawn using only a compass and straightedge.
• 1796 – Adrien-Marie Legendre suggested the prime number theorem.
• 1797 – Caspar Wessel connected vectors with complex numbers.
• 1799 – Carl Friedrich Gauss proved the fundamental theorem of algebra, which states that every polynomial equation has a solution among the complex numbers.
• 1799 – Paolo Ruffini partially proved that equations of the fifth degree or higher cannot be solved by a general formula.

19th Century: Deeper Understanding and New Concepts

• 1801 – Carl Friedrich Gauss's number theory book, Disquisitiones Arithmeticae, was published.
• 1805 – Adrien-Marie Legendre introduced the method of least squares for fitting curves to data.
• 1807 – Joseph Fourier discovered his trigonometric decomposition of functions.
• 1817 – Bernard Bolzano presented the intermediate value theorem for continuous functions.
• 1821 – Augustin-Louis Cauchy published Cours d'Analyse, an important work in analysis.
• 1824 – Niels Henrik Abel partially proved that general quintic (fifth-degree) or higher equations cannot be solved by simple formulas.
• 1825 – Augustin-Louis Cauchy introduced the theory of residues in complex analysis.
• 1829 – János Bolyai, Gauss, and Lobachevsky independently invented non-Euclidean geometry, which challenged Euclid's parallel postulate.
• 1832 – Évariste Galois presented a general condition for solving algebraic equations, founding group theory and Galois theory.
• 1837 – Pierre Wantzel proved that doubling the cube and trisecting the angle are impossible with only a compass and straightedge.
• 1843 – William Hamilton discovered quaternions, a type of number that is non-commutative (order matters in multiplication).
• 1844 – Hermann Grassmann published his Ausdehnungslehre, which led to linear algebra.
• 1847 – George Boole formalized symbolic logic in The Mathematical Analysis of Logic, creating Boolean algebra.
• 1854 – Bernhard Riemann introduced Riemannian geometry.
• 1858 – August Ferdinand Möbius invented the Möbius strip, a surface with only one side.
• 1859 – Bernhard Riemann formulated the Riemann hypothesis, a very important unsolved problem about prime numbers.
• 1868 – Eugenio Beltrami showed that Euclid’s parallel postulate is independent of the other axioms of Euclidean geometry.
• 1872 – Richard Dedekind invented the Dedekind Cut for defining irrational numbers.
• 1873 – Charles Hermite proved that the mathematical constant e is transcendental (not a root of any non-zero polynomial equation with integer coefficients).
• 1874 – Georg Cantor proved that the set of all real numbers is uncountably infinite, meaning it's a bigger kind of infinity than the set of counting numbers.
• 1882 – Ferdinand von Lindemann proved that π is transcendental, meaning a circle cannot be squared with a compass and straightedge.
• 1882 – Felix Klein invented the Klein bottle, another strange surface with no inside or outside.
• 1895 – Georg Cantor published a book on set theory, including the arithmetic of infinite cardinal numbers.
• 1895 – Henri Poincaré published "Analysis Situs", which started modern topology (the study of shapes and spaces).
• 1896 – Jacques Hadamard and Charles Jean de la Vallée-Poussin independently proved the prime number theorem.
• 1899 – David Hilbert presented a set of self-consistent geometric axioms in Foundations of Geometry.
• 1900 – David Hilbert stated his list of 23 problems, which guided much of 20th-century mathematical research.

Contemporary Math: The 20th and 21st Centuries

This period saw huge advancements, including the rise of computers and new ways to think about math.

20th Century: Computers and New Frontiers

• 1901 – Henri Lebesgue published on Lebesgue integration, a new way to define integrals.
• 1908 – Ernst Zermelo created set theory axioms to avoid contradictions.
• 1912 – Luitzen Egbertus Jan Brouwer presented the Brouwer fixed-point theorem.
• 1915 – Emmy Noether proved her symmetry theorem, showing that every symmetry in physics has a matching conservation law.
• 1928 – John von Neumann began developing game theory.
• 1931 – Kurt Gödel proved his incompleteness theorem, showing that any consistent system of math axioms will always have true statements that cannot be proven within that system.
• 1936 – Alonzo Church and Alan Turing created the λ-calculus and the Turing machine, which formalized the idea of computation.
• 1940 – Kurt Gödel showed that the continuum hypothesis and the axiom of choice cannot be disproven from standard set theory axioms.
• 1945 – Saunders Mac Lane and Samuel Eilenberg started category theory, a way to study mathematical structures and relationships.
• 1947 – George Dantzig published the simplex method for linear programming, used for optimization problems.
• 1948 – Claude Shannon developed the concept of Information Theory.
• 1949 – John Wrench and L.R. Smith computed π to 2,037 decimal places using the ENIAC computer.
• 1950 – Stanisław Ulam and John von Neumann introduced cellular automata, simple models that can show complex behavior.
• 1956 – Noam Chomsky described a hierarchy of formal languages.
• 1957 – Kiyosi Itô developed Itô calculus, important for financial math and physics.
• 1960 – Tony Hoare invented the quicksort algorithm, a very efficient way to sort data.
• 1960 – Rudolf Kalman introduced the Kalman Filter, used for estimating system states from noisy measurements.
• 1961 – Daniel Shanks and John Wrench computed π to 100,000 decimal places using an IBM-7090 computer.
• 1963 – Paul Cohen showed that the continuum hypothesis and the axiom of choice cannot be proven from standard set theory axioms.
• 1963 – Edward Norton Lorenz discovered chaotic behaviour and the Lorenz Attractor, leading to the idea of the Butterfly Effect.
• 1965 – Lotfi Asker Zadeh founded fuzzy set theory and the field of Fuzzy mathematics, which deals with uncertainty.
• 1965 – James Cooley and John Tukey presented an important fast Fourier transform algorithm.
• 1967 – Robert Langlands formulated the influential Langlands program, connecting number theory and representation theory.
• 1975 – Benoit Mandelbrot published Les objets fractals, forme, hasard et dimension, introducing the concept of fractals.
• 1976 – Kenneth Appel and Wolfgang Haken used a computer to prove the Four color theorem, showing that any map can be colored with only four colors so that no two adjacent regions have the same color.
• 1983 – Gerd Faltings proved the Mordell conjecture, showing there are only a finite number of whole number solutions for each exponent of Fermat's Last Theorem.
• 1994 – Andrew Wiles proved Fermat's Last Theorem, a problem that had puzzled mathematicians for centuries.
• 1994 – Peter Shor formulated Shor's algorithm, a quantum algorithm for integer factorization that is much faster than classical algorithms.
• 1995 – Simon Plouffe discovered the Bailey–Borwein–Plouffe formula, which can find the nth binary digit of π without calculating the digits before it.
• 1998 – Thomas Callister Hales proved the Kepler conjecture, about the most efficient way to stack spheres.
• 2000 – The Clay Mathematics Institute proposed the seven Millennium Prize Problems, offering a million dollars for solving each one.

21st Century: Continued Breakthroughs

• 2002 – Manindra Agrawal, Nitin Saxena, and Neeraj Kayal presented the AKS primality test, a fast way to determine if a number is prime.
• 2003 – Grigori Perelman proved the Poincaré conjecture, one of the Millennium Prize Problems.
• 2004 – The classification of finite simple groups, a huge collaborative effort by many mathematicians over fifty years, was completed.
• 2013 – Yitang Zhang proved the first finite bound on gaps between prime numbers.
• 2014 – Project Flyspeck announced a computer-assisted proof of Kepler's conjecture.
• 2015 – Terence Tao solved the Erdős discrepancy problem.
• 2016 – Maryna Viazovska solved the sphere packing problem in dimension 8, and later for dimension 24.

See also

• History of mathematical notation explains Rhetorical, Syncopated and Symbolic
• Timeline of ancient Greek mathematicians
• Timeline of mathematical innovation in South and West Asia
• Timeline of mathematical logic
• Timeline of women in mathematics
• Timeline of women in mathematics in the United States