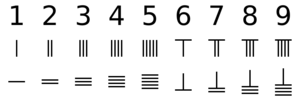
History of mathematical notation facts for kids

Kids Encyclopedia Facts

The history of mathematical notation is all about how the symbols we use in math today came to be! It shows how these symbols started, how they changed over time, and how they spread around the world. Mathematical notation is simply the set of symbols used to write math problems and formulas. These symbols help us represent numbers and operations clearly.

This history includes numbers like the ones we use every day (called Hindu–Arabic numerals), letters from different alphabets (like Roman, Greek, and Hebrew), and many other special symbols that mathematicians have invented over hundreds of years.

The way mathematical notation developed can be split into three main stages:

The rhetorical stage: In this early time, people did math using only words, with no special symbols at all.
The syncopated stage: Here, people started using short forms or abbreviations for common math operations and numbers.
The symbolic stage: This is when full systems of mathematical symbols took over from just using words or abbreviations. This stage began in Italy in the 1500s and has continued to grow and change ever since.

The study of how math symbols and methods developed in the past is a big part of the history of mathematics.

Math in Words: The Rhetorical Stage

In ancient times, people mostly did math using words. Even though the Greeks are often credited with early math, they learned a lot from the Ancient Egyptians and Ancient Phoenicians. The way numbers were written, with symbols having different values depending on their place (like in our number system), shows how advanced these early civilizations were.

Our knowledge of how these ancient people did math is not perfect, but we know they were very skilled. Many math ideas started from solving real-world problems. For example, geometry began with measuring distances and areas, and algebra grew from finding ways to solve problems with numbers.

Most early civilizations that left records knew about counting and basic mechanics. Some also knew about land-surveying. The Egyptians were good at geometry and numbers, while the Phoenicians focused on practical math, keeping records, and navigation. Their knowledge came from many years of observing and measuring things.

How Notation Began

Babylonian tablet (around 1800–1600 BCE) showing an early way to write the square root of 2.

The very first written math used tally marks. Each mark stood for one unit, like one animal or one person. These marks were often cuts in wood or stone, and everyone could understand them. The Greeks, who started using notation in Western history, likely learned from people living near the Mediterranean Sea, especially the Egyptians and Phoenicians.

The Ancient Egyptians used hieroglyphic symbols for numbers. They had symbols for one, ten, one hundred, and so on, all the way up to one million. Smaller numbers were placed on the left, just like in our modern number system. Later, Egyptians used a more cursive style called hieratic script for numbers. This script replaced groups of symbols with single ones, making it faster to write. For example, four vertical lines for the number four became a single horizontal line. We can see this in ancient texts like the Rhind Mathematical Papyrus. The Egyptians also had symbols for basic math operations: legs walking forward meant addition, and legs walking backward meant subtraction.

The Mesopotamians also had symbols for powers of ten. Later, they wrote numbers in a way very similar to modern times. Instead of a symbol for each power of ten, they used a number to show how many of that power there were. Digits were separated by a space. By the time of Alexander the Great, they even had a symbol for zero, which acted as a placeholder. The Mesopotamians used a sexagesimal system, which means it was based on the number sixty. This is why we have 60 seconds in a minute, 60 minutes in an hour, and 360 degrees in a circle today!

Most Mesopotamian clay tablets we've found are from 1800 to 1600 BCE. They cover topics like fractions, algebra, and how to solve different types of equations. These tablets also include multiplication tables. Unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system. This means a digit's value changed based on its position, just like in our decimal system. However, they didn't have a symbol like our decimal point, so you had to guess the place value from the problem's context.

Shortcuts and Symbols: The Syncopated Stage

Archimedes Thoughtful by Fetti (1620).

The history of mathematics as a formal subject really begins with the Pythagoreans in the 6th century BCE. They even created the word "mathematics." Greek math started with geometry and was very logical and scientific. For example, Pythagoras is often credited with the Pythagorean theorem, which explains the relationship between the sides of a right-angled triangle.

Plato had a big impact on math and science. He helped separate "arithmetic" (which is now called number theory) from "logistic" (which is now called basic arithmetic). Greek mathematics greatly improved math methods by introducing deductive reasoning and strict proofs.

Abstract Mathematics deals with numbers and quantities in a general way, without thinking about specific objects. Examples include arithmetic and geometry. This is different from applied mathematics, where math ideas are used to solve problems in the real world, like in hydrostatics (the study of fluids) or navigation.

Archimedes is considered one of the greatest mathematicians of all time. He found ways to calculate areas and volumes, and he gave a very accurate estimate for pi. He also invented a clever system for writing very large numbers.

Euclid's Elements.

The ancient Greeks made big steps in making geometry more abstract. Euclid's Elements (around 300 BCE) is one of the oldest Greek math books we still have. It's a collection of definitions, rules, theorems, and proofs. This book was very important for developing logic, math, and science.

Diophantus of Alexandria wrote books called Arithmetica, which focused on solving algebraic equations. He was one of the first to use symbols in equations, though not as much as we do today. For example, he used 's' for an unknown number.

Greek Ways of Writing Numbers

The ancient Greeks used a system called Attic numeration, which was similar to the Egyptian system and later used by the Romans. Numbers one through four were vertical lines. The symbol for five was the Greek letter Π (pi), which is the first letter of the Greek word for five, pente. Numbers six through nine used Π with vertical lines next to it. Ten was represented by the letter Δ (delta), from the word for ten, deka, and so on.

The Ionian numeration system used all 24 letters of the Greek alphabet, plus three older letters. This system was much more organized than the Roman system. The Greeks divided their alphabet into three groups, and by adding extra symbols, they had characters for units, tens, and hundreds.

Α (α)	Β (β)	Г (γ)	Δ (δ)	Ε (ε)	Ϝ (ϝ)	Ζ (ζ)	Η (η)	θ (θ)	Ι (ι)	Κ (κ)	Λ (λ)	Μ (μ)	Ν (ν)	Ξ (ξ)	Ο (ο)	Π (π)	Ϟ (ϟ)	Ρ (ρ)	Σ (σ)	Τ (τ)	Υ (υ)	Φ (φ)	Χ (χ)	Ψ (ψ)	Ω (ω)	Ϡ (ϡ)
1	2	3	4	5	6	7	8	9	10	20	30	40	50	60	70	80	90	100	200	300	400	500	600	700	800	900

This system appeared around the 3rd century BCE. When lowercase letters came into use, they were also used for numbers. To write thousands, they put a stroke in front of the number (e.g., ",α" for one thousand).

Greek mathematicians mostly focused on geometry, so they didn't use many symbols for algebra. Diophantus was an exception, using some symbols in his Arithmetica.

Chinese Mathematical Notation

The numbers 0–9 in Chinese huāmǎ (花碼) numerals.

The Chinese used numerals that looked a lot like tally marks. Numbers one through four were horizontal lines. Five was an X between two horizontal lines. Today, the huāmǎ system is mainly used for prices in Chinese markets or on old handwritten invoices.

Mathematics in China developed independently by the 11th century BCE. The Chinese were skilled in arithmetic, geometry, mechanics, and astronomy. They developed very large and negative numbers, decimals, a place value system, a binary system, algebra, geometry, and trigonometry.

Counting rod numerals.

Chinese math made early contributions, including a place value system. They used counting rods for calculations. Our knowledge of early Chinese math is better than for some other ancient cultures, and it shows that a nation can be very skilled in practical arts even if we don't know much about the advanced math behind them.

Ancient Chinese mathematicians didn't use an axiomatic approach (starting with basic truths), but they made progress in developing algorithms and algebra. Chinese algebra reached its peak in the 13th century.

Because of language and distance, Chinese math and ancient Mediterranean math developed mostly on their own. However, some ideas likely spread across Asia. Many early math ideas, like the Pythagorean theorem, were known in China centuries ago. Pascal's triangle was also known in China long before Blaise Pascal.

A modern artist's drawing of Shen Kuo.

Trigonometry in China began to advance during the Song Dynasty (960–1279). Chinese mathematicians like Shen Kuo (1031–1095) used trigonometric functions to solve problems with circles. Later, Guo Shoujing (1231–1316) used spherical trigonometry to improve the Chinese calendar and astronomy. Arab missionaries also brought knowledge of spherical trigonometry to China in the 13th century.

Indian and Arabic Numerals

Image-Al-Kitāb al-muḫtaṣar fī ḥisāb al-ğabr wa-l-muqābala

A page from al-Khwārizmī's Algebra.

Our modern number system, the Hindu–Arabic numeral system, has ancient roots in India. It was used by Hindus over two thousand years ago. The Indian mathematician Brahmagupta used a "syncopated" algebraic notation. He showed addition by placing numbers side by side, subtraction with a dot over the number to be subtracted, and division by placing the divisor below the dividend (like a fraction, but without the line).

Even though we call them "Arabic numerals," they actually came from India. Europeans saw these numbers in an Arabic book by Muhammed ibn-Musa al-Khwarizmi. Al-Khwarizmi wrote important books about the Hindu–Arabic numerals and how to solve equations. His book On the Calculation with Hindu Numerals (around 825 CE) helped spread Indian math to the West. The word algorithm comes from Al-Khwarizmi's name, and algebra comes from the title of one of his books.

Islamic mathematics expanded on the math known to Central Asian civilizations. Al-Khwarizmi explained how to solve quadratic equations. He also discussed methods of "reduction" and "balancing" equations, which means moving terms to the other side of an equation or canceling out similar terms.

Later, Al-Karaji expanded these methods to include powers and roots of unknown numbers. Abul Wafa translated the works of Diophantus into Arabic. Ibn al-Haytham developed analytic geometry. Omar Khayyam developed algebraic geometry and wrote about solving cubic equations. Muslim mathematicians also added the decimal point to Arabic numerals.

The modern Arabic numeral symbols we use today first appeared in Islamic North Africa in the 10th century. These are the direct ancestors of the numbers used worldwide.

Many Greek and Arabic math texts were later translated into Latin. This led to more math development in medieval Europe. In the 12th century, scholars traveled to Spain and Sicily to find Arabic scientific texts, including Al-Khwarizmi's work and Euclid's Elements. One important European book that promoted using these new numerals was Liber Abaci by Fibonacci. This book is also famous for a math problem Fibonacci wrote about rabbits, which led to the Fibonacci sequence.

Symbols Take Over: The Symbolic Stage

Symbols by popular introduction date

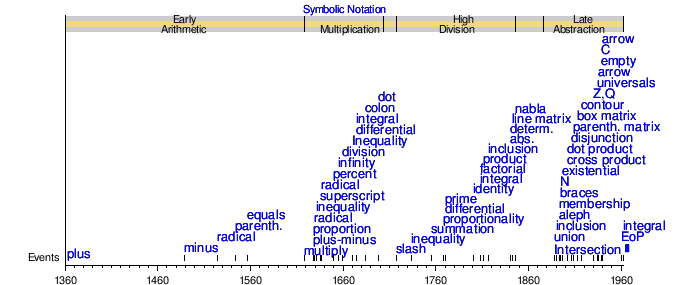
Early Arithmetic and Multiplication Symbols

The shift to using only symbols in algebra began with mathematicians like Ibn al-Banna' al-Marrakushi (1256–1321) and Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī (1412–1482). Al-Qalasadi's notation was the first to use symbols for math operations, which was a big step towards modern algebraic symbols.

The 1489 use of the plus and minus signs in print.

The two most common arithmetic symbols, plus (+) and minus (−), appeared in the 14th and 15th centuries. The plus sign was used around 1360 by Nicole Oresme. It might have come from an abbreviation for "et," meaning "and" in Latin. The minus sign was used in 1489 by Johannes Widmann in his book Mercantile Arithmetic. Widmann used these symbols to show deficits and surpluses.

In the 15th century, Ghiyath al-Kashi calculated π to many decimal places. Mathematicians like Scipione del Ferro and Niccolò Fontana Tartaglia found ways to solve cubic equations. Gerolamo Cardano published these solutions in his book Ars Magna in 1545. The radical symbol for square roots was introduced by Christoph Rudolff.

In 1556, Niccolò Tartaglia used parentheses for grouping operations. In 1557, Robert Recorde introduced the equals sign (=) to English readers in his book The Whetstone of Witte. In 1564, Gerolamo Cardano started studying probability theory by analyzing games of chance.

John Napier is famous for inventing logarithms and making the decimal point common in math. In 1622, William Oughtred invented the slide rule, which uses sliding scales to do multiplication and division. In 1631, Oughtred also introduced the multiplication sign (×) and the abbreviations sin and cos for sine and cosine functions.

René Descartes is known as the father of analytical geometry, which connects algebra and geometry. In the 17th century, Descartes introduced Cartesian co-ordinates, which allowed for the development of analytic geometry. Blaise Pascal described binomial coefficients in his "Treatise on the Arithmetical Triangle" in 1653. John Wallis introduced the infinity symbol. In 1659, Johann Rahn introduced the division sign (÷).

In 1706, William Jones used the Greek letter π to represent pi because it's the first letter of the Greek word for "perimeter." This use became popular thanks to Leonhard Euler in 1737.

Calculus Notation: Leibniz and Newton

Derivative notations
Sir Isaac Newton Gottfried Wilhelm Leibniz

Calculus had two main systems of notation, created by its two founders: Isaac Newton and Gottfried Leibniz. Leibniz's notation is the one used most often today. Newton's notation used a dot or dash above a function to show its derivative. This is still used today, especially in physics, to show how things change over time.

Leibniz, on the other hand, used the letter 'd' as a prefix for differentiation. He also introduced the integral symbol, which looks like a long 'S'. This 'S' stands for Summa, meaning "sum" in Latin. When finding areas under curves, integration adds up the areas of many tiny rectangles, so the 'S' makes sense.

Later Symbols and Functions

In this period, letters of the alphabet became widely used as symbols for quantities. The first letters of the alphabet (like a, b, c) often stood for coefficients (numbers that multiply variables), and the last letters (like x, y, z) stood for unknowns. Certain letters, like π and e, became universally accepted for specific numbers (like 3.14159... and 2.71828...).

In 1718, Thomas Twinin started using the slash (/) for division, which came from the earlier Arabic horizontal fraction bar.

Euler and Prime Notations

Leonhard Euler's signature.

Leonhard Euler was one of the most important mathematicians in history and invented many common math symbols. He used e for the base of natural logarithms. He also consistently used π for pi, as suggested by William Jones. Euler used i to represent the square root of negative one. For summation (adding many numbers), Euler used the Greek letter sigma, Σ. He also introduced the notation 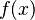$f(x)$ to represent a function of $x$ .

Joseph-Louis Lagrange created the prime symbol (like 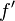$f'$ ) for derivatives.

Gauss, Hamilton, and Matrix Notations

Around the early 1800s, Carl Friedrich Gauss developed the identity sign (≡) for congruence relations. He also developed the product sign (Π) for multiplying many terms.

After the 1800s, Christian Kramp promoted factorial notation (like 5!). Joseph Diaz Gergonne introduced set inclusion signs (like ⊂). Karl Weierstrass helped define the concept of absolute value and the determinant of a matrix.

Matrix notation was further developed by Arthur Cayley. He used a single letter to represent a whole matrix, treating it as one object. He also saw the link between matrices and determinants.

William Rowan Hamilton introduced the nabla symbol (∇) for vector differentials. He also invented quaternion notation. Hamilton introduced the word "tensor" in 1846. James Joseph Sylvester introduced the term "matrix" into matrix algebra in 1848.

Maxwell, Clifford, and Ricci Notations

James Clerk Maxwell formulated a set of equations that combined electricity, magnetism, and optics.

In 1864, James Clerk Maxwell put all the known information about electromagnetism into a set of differential equations. In 1878, William Kingdon Clifford separated the dot product and cross product of vectors from the more complex quaternion notation. This made vector calculus easier for engineers to use.

Tensor calculus was developed by Gregorio Ricci-Curbastro between 1887 and 1896. In 1895, Henri Poincaré published Analysis Situs, which was important for topology (the study of shapes and spaces).

From Formulas to Tensors

In 1895, Giuseppe Peano created his Formulario mathematico, trying to write math in a very short way using special symbols. He defined a vector space and linear map. He also introduced the intersection sign (∩), the union sign (∪), the membership sign (∈, "is an element of"), and the existential quantifier (∃, "there exists"). Peano's work greatly influenced Bertrand Russell, who, with Alfred North Whitehead, wrote Principia Mathematica, a very important book that made symbols central to modern math.

Mathematical Logic and Abstraction

Abstraction
Felix Klein Georg Cantor

At the start of the 20th century, Felix Klein's "Erlangen program" showed how different geometries were connected by studying properties that stayed the same under certain symmetries. This abstract thinking linked geometry with abstract algebra. Georg Cantor introduced the aleph symbol (ℵ) for the sizes of infinite sets. His notation is still used today.

After 1900, Josiah Willard Gibbs introduced the middle dot (⋅) for the dot product and the multiplication sign (×) for cross products in physical chemistry. Bertrand Russell introduced logical disjunction (∨, "OR") in 1906. Later, different matrix notations were introduced.

Gödel's Incompleteness Notation

While proving his incompleteness theorems, Kurt Gödel created a unique way to represent logical statements using numbers, called Gödel numbers. He assigned numbers to operations and variables. Then, he multiplied prime numbers raised to the power of these numbers to create a single, unique number for every logical statement. This showed that every logic statement could have its own number.

Modern Notation and Topics

Early 20th-Century Notation

The abstraction of notation is still happening. Many set notations were developed for fundamental sets. In the 1920s, Paul Adrien Maurice Dirac made important contributions to quantum mechanics, introducing the concept of creation and annihilation operators for particles. He also formulated the Dirac equation to describe the behavior of electrons moving at high speeds.

In the 1930s, special double-struck capital letters were created for number sets: ℤ for integers, ℚ for rational numbers, and ℂ for complex numbers. In 1935, Gerhard Gentzen introduced universal quantifiers (∀, "for all"). André Weil and Nicolas Bourbaki developed the empty set sign (∅) in 1939.

The arrow symbol (→) was developed for function notation in 1936 by Øystein Ore to show how elements are mapped. Later, in 1940, it took its current form, like f: X → Y, through the work of Witold Hurewicz.

Paul Dirac made big contributions to quantum mechanics.

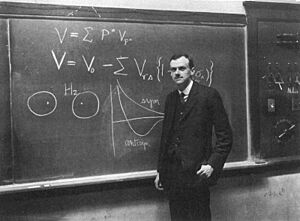
Bra–ket notation (Dirac notation) is a standard way to describe quantum states. It uses angle brackets and vertical bars, like ⟨φ|ψ⟩. This notation was introduced in 1939 by Paul Dirac. It's used in almost all of quantum mechanics and helps explain how particles behave. The expression ⟨φ|ψ⟩ is often seen as the probability amplitude for one state to change into another.

In the 1960s, set-builder notation was developed to describe a set by listing the properties its members must have. Also, tensors were made more abstract using category theory. Later, multi-index notation was created to simplify writing in multivariable calculus and partial differential equations.

Modern Mathematical Notation

In modern math, especially in special relativity and electromagnetism, the d'Alembert operator is used. The Levi-Civita symbol is used in tensor calculus.

In 1965, Sin-Itiro Tomonaga, Julian Schwinger, and Richard Feynman won the Nobel Prize in Physics for their work on quantum electrodynamics. Feynman's method, using his famous diagrams, was a new way to understand particle interactions.

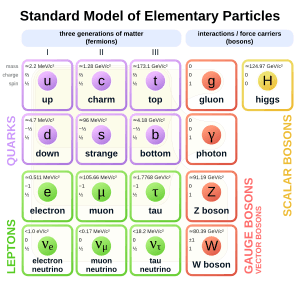
The Standard Model of Elementary Particles, showing fundamental particles.

A big step towards the Standard Model of particle physics was Sheldon Glashow's discovery in 1960 of how to combine the electromagnetic and weak interactions. In 1967, Steven Weinberg and Abdus Salam added the Higgs mechanism to Glashow's theory, giving it its modern form. The Higgs mechanism is thought to give mass to all elementary particles.

In the late 1970s, William Thurston introduced hyperbolic geometry into the study of knot theory. The orbifold notation system, invented by Thurston, helps classify symmetry groups in two-dimensional spaces.

The first superstring revolution happened between 1984 and 1986. Vaughan Jones discovered the Jones polynomial, which showed deep connections between knot theory and quantum field theory. According to string theory, all particles come from tiny vibrating strings.

In the 1990s, Roger Penrose proposed Penrose graphical notation (also called tensor diagram notation) as a visual way to represent multilinear functions or tensors. He also introduced abstract index notation. In 1995, Edward Witten suggested M-theory, which helped explain some dualities in string theory, starting the second superstring revolution.

John H Conway, a mathematician known for his notations.

John Conway developed several notations, including the Conway chained arrow notation for very large numbers and the Conway notation for knot theory. The Coxeter notation system classifies symmetry groups.

Computers and Markup Notation

A section of a quintic Calabi–Yau three-fold, an abstract visualization.

The rise of computers has brought mathematical notation full circle. Now, symbols can be used in abstract visualizations, like showing projections of a Calabi–Yau manifold. These computer graphics help us understand complex mathematical ideas that might not have a direct real-world example.

In 1931, IBM created the IBM 601 Multiplying Punch, an early electromechanical machine that could multiply numbers. In 1936, Alan Turing published his famous paper "On Computable Numbers," which laid the groundwork for computer science. John von Neumann was a pioneer of the digital computer.

In 1962, Kenneth E. Iverson developed APL, a programming language for working with arrays. In the 1970s, Edgar F. Codd proposed relational algebra for database query languages. Today, there are many C mathematical functions and numerical libraries used in software development for math calculations. Programs like Mathematica and SymPy are based on symbolic mathematics.

Future of Mathematical Notation

The history of mathematical notation shows a constant move from concrete ideas to abstract ones. With computer visualization systems, we can now apply these notations to abstract images, like those of a Calabi–Yau manifold. This helps us understand math concepts that involve random variables or other complex ideas.