Mathematics and art facts for kids
Mathematics and art are connected in many cool ways! Math itself can be seen as an art because of its beauty. You can find math in things like music, dance, painting, architecture, sculpture, and even textiles. This article will mostly look at how math appears in visual arts like paintings and sculptures.
Math and art have a long history together. Artists have used math for thousands of years. For example, in ancient Greece, the sculptor Polykleitos wrote a guide called his Canon about the perfect body shapes for statues. Some people think he used a special ratio (1:√2) for ideal male figures.
During the Italian Renaissance, a mathematician named Luca Pacioli wrote a famous book called De divina proportione (1509). It was about using the golden ratio in art and had amazing drawings by Leonardo da Vinci. Another Italian painter, Piero della Francesca, used Euclid's ideas to develop perspective in his paintings and writings. The artist Albrecht Dürer also included many math ideas in his work.
In more recent times, the artist M. C. Escher used lots of tessellation (patterns that fit together without gaps) and hyperbolic geometry in his art, sometimes with help from mathematician H. S. M. Coxeter. The De Stijl art movement, led by Theo van Doesburg and Piet Mondrian, loved using simple geometric shapes.
Math has also inspired textile arts like quilting, knitting, cross-stitch, and weaving. In Islamic art, you can see amazing symmetries in things like Persian girih tiles, Moroccan zellige patterns, and muqarnas (fancy ceiling designs).
Math gives artists tools like linear perspective (making things look 3D on a flat surface), understanding symmetry, and using mathematical shapes like polyhedra (3D shapes with flat faces) and the Möbius strip (a strip with only one side). Even Computer art often uses fractals, like the Mandelbrot set, which are complex patterns that repeat themselves.
Some experts, like artist David Hockney, believe that Renaissance artists used tools like the camera lucida to draw very accurately. Architect Philip Steadman thinks Vermeer used the camera obscura for his detailed paintings.
Math can also help us study art. For example, scientists have used math to analyze traditional batik fabrics from Java and found they have different fractal dimensions (a way to measure how complex a pattern is).
Contents
Ancient Connections: From Greece to the Renaissance
Artists have always looked for ways to make their work look real and beautiful. Math helped them do this.
Polykleitos and Perfect Proportions
Polykleitos (around 450–420 BC) was a famous Greek sculptor. He made amazing bronze statues of athletes. He wrote a guide called the Canon to show how to sculpt the "perfect" male body.
The Canon itself is lost, but people believe Polykleitos used a series of proportions. Each length was like the diagonal of a square drawn on the previous length, using the ratio 1:√2 (about 1:1.4142). This idea of "harmonious proportions" (called symmetria in Greek) was a mathematical way to describe the human form.
Polykleitos's ideas greatly influenced Greek, Roman, and Renaissance sculptors. Even though his original statues are gone, Roman copies show his ideal of physical perfection and mathematical accuracy.
Perspective and Depth in Art
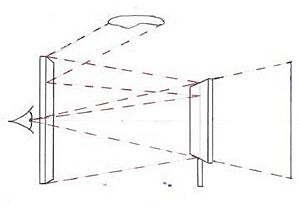
In ancient times, painters often made important figures bigger, no matter how far away they were. In the Middle Ages, some artists even used "reverse perspective" to make things stand out.
During the Renaissance, people rediscovered old Greek and Roman ideas, including using math to understand nature and art. Artists wanted to show 3D scenes on a flat canvas. Also, many believed that math was the key to understanding the universe, and that art could be explained with geometry.
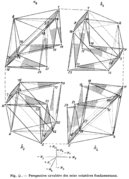
Giotto (1266–1337) was one of the first to try drawing with perspective. In 1415, the Italian architect Filippo Brunelleschi and his friend Leon Battista Alberti showed a geometric way to use perspective in Florence. They used similar triangles (shapes that are the same but different sizes) to figure out how tall distant objects should appear. Brunelleschi's own perspective paintings are lost, but you can see his ideas in Masaccio's Holy Trinity painting.
_01.jpg)
The Italian painter Paolo Uccello (1397–1475) loved perspective. His paintings of The Battle of San Romano clearly show this, with broken spears lying perfectly along perspective lines.
Piero della Francesca (around 1415–1492) was another important artist who was also a great mathematician. He wrote books about solid geometry and perspective, like De prospectiva pingendi (On Perspective for Painting). His interest in perspective is clear in his paintings, such as The Flagellation of Christ.
In 1435, Alberti explained linear perspective like this: "Light rays travel in straight lines from points in the scene to the eye, forming a kind of pyramid with the eye at the top." A painting made with linear perspective is like a slice through that pyramid.
Some art historians, like David Hockney, suggest that artists started using tools like the camera lucida (a device that projects an image onto paper) in the 1420s to draw more precisely. Others, like Philip Steadman, think Vermeer used a camera obscura (a dark box with a lens) for his unique paintings.
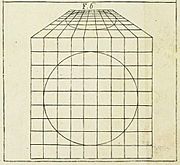
In 1509, Luca Pacioli published De divina proportione, which was about math and art proportions, including in the human face. Leonardo da Vinci (1452–1519) drew the pictures for this book, including some of the first drawings of 3D shapes called "skeletonic solids." Leonardo also used linear perspective in famous works like Mona Lisa and The Last Supper. His Vitruvian Man drawing shows a man perfectly fitting inside both a circle and a square, based on ideas from the Roman architect Vitruvius.
Artists also explored curvilinear perspective, which makes images look distorted. Jan van Eyck's 1434 Arnolfini Portrait has a convex mirror showing reflections of the scene. Parmigianino's Self-portrait in a Convex Mirror (around 1523–1524) shows his face clearly in the middle, but the background is strongly curved.
-
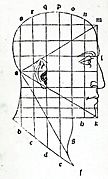
A woodcut from Luca Pacioli's 1509 book De divina proportione, showing an equilateral triangle on a human face.
-
A camera lucida being used to draw in 1879.
-
An illustration from the 1600s showing an artist using a camera obscura.
-
Brunelleschi's ideas about perspective are shown in Masaccio's Trinità, around 1426–1428.
-
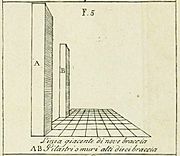
A diagram from Leon Battista Alberti's 1435 book Della Pittura, showing pillars in perspective on a grid.
-
Linear perspective in Piero della Francesca's Flagellation of Christ, around 1455–1460.
-
Curvilinear perspective: a convex mirror in Jan van Eyck's Arnolfini Portrait, 1434.
-
Parmigianino, Self-portrait in a Convex Mirror, around 1523–1524.
-
Pythagoras with a tablet of ideal ratios, from Raphael's The School of Athens, 1509.
-
Oblique projection: Entrance and yard of a yamen. A detail from a Chinese scroll from the 1700s.
-
Oblique projection: women playing board games. A Japanese painting by Torii Kiyonaga, around 1780.
.jpg)
The Golden Ratio in Art
The golden ratio (about 1.618) was known to the Greek mathematician Euclid. In modern times, many people have claimed that ancient artists and architects in Egypt and Greece used the golden ratio in their work. However, there isn't strong proof for these claims. For example, the Parthenon temple in Athens has been said to use the golden ratio, but measurements don't support this.
After Pacioli's book in 1509, the golden ratio became more clearly visible in artworks, including Leonardo's Mona Lisa.
-
Different ideas for the base-to-hypotenuse ratios of the Pyramid of Khufu.
-
Supposed ratios in Notre-Dame of Laon.
-
Golden rectangles placed on the Mona Lisa to show where the golden ratio might appear.
-
The 1967 St. Benedictusberg Abbey church by Hans van der Laan uses proportions based on the plastic number.
Symmetry in Patterns
Symmetry has been used in art for thousands of years, especially in carpets, textiles, and tiles.
Many traditional rugs, like kilims, have a central area and a border. Both often show symmetry, even if small details are slightly different because they are handmade. In kilims from Anatolia, the patterns themselves are usually symmetrical. Weavers definitely wanted symmetry, even if they didn't know the exact math behind it.
The mathematician Nikos Salingaros thinks that the "powerful presence" of a great carpet comes from mathematical ideas. These include using opposite colors, balancing shapes, adding small details, and repeating elements at different sizes.
Intricate patterns are also found in Indian Jali work, which are marble screens used in tombs and palaces. Chinese patterns also show symmetry and can be found in many different wallpaper groups (mathematical ways to classify repeating patterns).
Symmetries are very important in textile arts like quilting, knitting, and embroidery. Rotational symmetry (where a shape looks the same after being turned) is seen in circular structures like domes, which are often decorated with symmetric patterns.
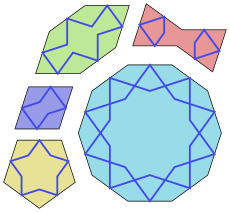
Islamic art uses symmetries a lot, especially in girih patterns. These patterns are made from five specific tile shapes, all with sides of the same length and angles that are multiples of 36 degrees. This creates patterns with five-fold and ten-fold symmetries. In 2007, scientists Peter Lu and Paul Steinhardt suggested that girih patterns look like quasicrystalline Penrose tilings, which are patterns that never perfectly repeat.
-
A Hotamis kilim (detail) from central Anatolia, early 1800s.
-
A detail of a Ming Dynasty brocade, showing a hexagonal pattern.
-
A Jaali marble screen at the tomb of Salim Chishti, India.
-
Symmetries in Florentine Bargello pattern tapestry work.
-
The ceiling of the Sheikh Lotfollah Mosque, Isfahan, 1619.
-
Rotational symmetry in lace made with tatting work.
-
Girih tiles: patterns on a wall from the Darb-i Imam shrine, Isfahan, 1453.
-
Tessellations: zellige mosaic tiles at Bou Inania Madrasa, Fes, Morocco.
-
The complex geometry and tiles of the muqarnas vaulting in the Sheikh Lotfollah Mosque, Isfahan.
-
An architect's plan of a muqarnas vault from the Topkapı Scroll.
2.jpg)
Polyhedra in Art
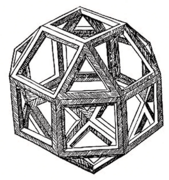
Platonic solids and other polyhedra (3D shapes with flat faces) appear often in Western art. You can find them in a mosaic in Venice, in Leonardo da Vinci's drawings for Pacioli's book, and in Albrecht Dürer's famous engraving Melencolia I.
Albrecht Dürer (1471–1528) was a German artist who wrote important books about polyhedra. His 1525 book, Underweysung der Messung (Education on Measurement), taught about linear perspective, geometry in architecture, and Platonic solids. Dürer was also the first to show how to "unfold" a polyhedron into a flat shape, called a polyhedral net, for printing.
Dürer's Melencolia I shows a thinker next to a special 3D shape and a magic square. These objects have been studied and interpreted by many people.
Salvador Dalí's 1954 painting Corpus Hypercubus shows Christ's cross as an unfolded hypercube (a 4D cube). This is like unfolding a regular cube into a cross shape made of six squares. The painting suggests a divine view of a four-dimensional shape.
-
The first printed drawing of a rhombicuboctahedron, by Leonardo da Vinci, from De Divina Proportione, 1509.
-
An Icosahedron as part of a monument to Baruch Spinoza in Amsterdam.
Fractal Patterns in Art
Traditional Indonesian batik designs, made with wax and dye on cloth, mix realistic patterns with abstract, slightly messy elements. Batik designs have a fractal dimension (a way to measure how complex a pattern is) between 1 and 2, depending on the region. For example, batik from Cirebon has a fractal dimension of 1.1, while batik from Yogyakarta has one between 1.2 and 1.5.
The "drip paintings" of modern artist Jackson Pollock also have unique fractal dimensions. His 1948 painting Number 14 has a fractal dimension of 1.45, and his later works had even higher dimensions, meaning more complex patterns.
The Deep Connection Between Math and Art
The famous astronomer Galileo Galilei once wrote that the universe is "written in the language of mathematics, and its characters are triangles, circles, and other geometric figures." He believed artists who study nature must first understand math. On the other hand, mathematicians have tried to understand art using geometry and logic.
Math as an Art Form Itself
Many mathematicians see math as an art. Jerry P. King says that "the keys to mathematics are beauty and elegance." He believes beauty is what drives mathematicians to do research. He mentions mathematician G. H. Hardy's essay A Mathematician's Apology, where Hardy talks about the beauty of proofs, like the one that shows there are endless prime numbers.
The Hungarian mathematician Paul Erdős agreed that math is beautiful but said it's hard to explain why. He compared it to asking why Beethoven's Ninth Symphony is beautiful – if you don't see it, no one can tell you.
Mathematical Tools for Artists
Math provides many tools for artists. For example, the rules of linear perspective help artists create depth. Artists like Luca Pacioli, Leonardo da Vinci, and Albrecht Dürer used and developed mathematical ideas in their art. The idea of the vanishing point in perspective was first explained by Brunelleschi around 1413, influencing later artists.
Isaac Newton's work on the optical spectrum (how light creates colors) influenced artists like J. M. W. Turner. Artists can also use math to analyze the symmetry of a scene.
Artists like M. C. Escher were inspired by math, especially by mathematician H. S. M. Coxeter. Even architects like Frank Gehry have used computer aided design to create new shapes in their buildings.
Some artists, like Richard Wright, see mathematical objects that can be built as "works of computer art." He points out that fractals were known to mathematicians for a century before artists recognized them.
Early computer art was made by machines, like Desmond Paul Henry's "Drawing Machine 1" in 1962, which made complex, abstract line drawings. More recently, artists like Hamid Naderi Yeganeh create shapes that look like real objects, like birds, using math formulas to draw many curves or lines. Mikael Hvidtfeldt Christensen creates generative or algorithmic art by writing computer code that applies mathematical operations to data.
-
A mathematical sculpture by Bathsheba Grossman, 2007.
-
A Fractal sculpture: 3D Fraktal 03/H/dd by Hartmut Skerbisch, 2003.
-
A detail of artwork by Samuel Monnier, 2009, based on a Fibonacci word.
-
A Computer art image made by Desmond Paul Henry's "Drawing Machine 1", shown in 1962.
-
A Bird in Flight, by Hamid Naderi Yeganeh, 2016, made with many mathematical curves.
From Math to Art Movements
The mathematician Henri Poincaré's book Science and Hypothesis was read by Cubist artists like Pablo Picasso. Poincaré knew that Euclidean geometry (the geometry we learn in school) was just one type of geometry. This idea, and the thought of a fourth dimension, made artists question traditional Renaissance perspective. This led to Cubism, an art movement that used mathematical ideas of color and form to create abstract art.
Mathematical models, which are often symmetrical and have interesting shapes, have inspired artists like the Dadaists Man Ray and Marcel Duchamp. Man Ray photographed mathematical models from a museum in Paris, calling them Objet mathematique. He said these forms were "as varied and authentic as any in nature."
Twentieth-century sculptors like Henry Moore and Barbara Hepworth also found inspiration in mathematical models. Moore said he was fascinated by the mathematical models at the Science Museum, especially how he could "look through the strings as with a bird cage and to see one form within another."
Artists Theo van Doesburg and Piet Mondrian started the De Stijl movement. They wanted to create art using simple geometric shapes that everyone could understand. Their art often used squares and triangles.
The graphic artist M. C. Escher (1898—1972) used the math of tessellations (patterns that fit together), polyhedra, and how space is shaped for his woodcuts. In his Alhambra Sketch, Escher showed that art can be made with regular shapes like triangles, squares, and hexagons. He also used irregular shapes and transformations like reflections to create his patterns. Many of his works show impossible constructions, which look strange but are fun to look at. Escher's Ascending and Descending is based on the "impossible staircase" created by Lionel and Roger Penrose.
Some of Escher's tessellation drawings were inspired by talks with mathematician H. S. M. Coxeter about hyperbolic geometry. Escher was especially interested in five specific polyhedra (the Platonic solids), which appear many times in his art.
The visual complexity of math shapes like tessellations and polyhedra has inspired many artists. Stewart Coffin makes polyhedral puzzles, and Magnus Wenninger creates beautiful models of complex stellated polyhedra.
The distorted views of anamorphosis have been used in art since the 1500s. Hans Holbein the Younger included a very stretched-out skull in his 1533 painting The Ambassadors.
The math of topology (the study of shapes that can be stretched or bent without tearing) has inspired modern artists. Sculptor John Robinson created works like Gordian Knot and Bands of Friendship, showing knot theory in bronze. Other works by Robinson explore the topology of toruses (doughnut shapes). Sculptor Helaman Ferguson creates complex surfaces and other topological objects that are visual representations of math.
The American weaver Ada Dietz wrote a book in 1949 about weaving patterns based on math formulas. Mathematician Daina Taimiņa showed how to crochet models of the hyperbolic plane in 2001. This led Margaret and Christine Wertheim to crochet a coral reef with many sea animals whose shapes are based on hyperbolic planes.
-
Four-dimensional space to Cubism: Esprit Jouffret's 1903 book Traité élémentaire de géométrie à quatre dimensions.
-
De Stijl: Theo van Doesburg's geometric Composition I (Still Life), 1916.
-
Pedagogy to art: Magnus Wenninger with some of his stellated polyhedra, 2009.
-
A Möbius strip scarf made in crochet, 2007.
-
Anamorphism: The Ambassadors by Hans Holbein the Younger, 1533, with a very distorted skull in the front.
-
A Crocheted coral reef: many animals modeled as hyperbolic planes by Margaret and Christine Wertheim. Föhr Reef, Tübingen, 2013.
Art Explaining Math Ideas
Art can also help explain math concepts. Giotto's Stefaneschi Triptych, from 1320, shows recursion (something that refers to itself). The painting shows a cardinal holding the very same painting as an offering!
René Magritte's surrealist paintings often play with logical puzzles. In La condition humaine (1933), Magritte paints an easel on the canvas, holding a painting that perfectly matches the view through a window, making you wonder what's real.
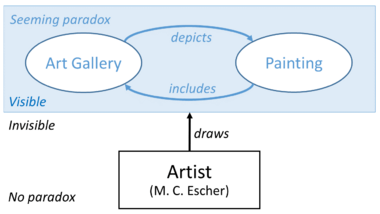
Similarly, Escher's Print Gallery (1956) is a print that shows a distorted city, which contains a gallery, which then seems to contain the picture itself, going on and on. This is a "strange loop" of reality.
Salvador Dalí's last painting, The Swallow's Tail (1983), was inspired by René Thom's catastrophe theory, which studies how small changes can lead to sudden, big changes.
The artist Adrian Gray creates amazing stone balancing sculptures. He uses friction and the center of gravity to make seemingly impossible compositions where rocks are stacked in delicate balance.
As Douglas Hofstadter wrote about Escher's art, it creates a feeling that "the end result is not reconcilable with one's conception of the world." The central empty space in Print Gallery has even led mathematicians to suggest it could contain a smaller, rotated copy of itself, showing even more recursion.
Art Inspiring Math Research
Sometimes, art has even helped math grow! Brunelleschi's ideas about perspective in art led to new research in math. This eventually resulted in the development of projective geometry by mathematicians like Girard Desargues.
The Japanese art of origami (paper-folding) has also been studied mathematically. People like Tomoko Fusé create complex shapes like polyhedra by folding many identical pieces of paper. Paper-folding was even used in 1893 to demonstrate geometric proofs.
-
This diagram by Leon Battista Alberti from 1435–1436 shows a circle seen in perspective as an ellipse, which helped lead to projective geometry.
Optical Illusions and Op Art
Optical illusions, like the Fraser spiral illusion, show how our eyes can be tricked. The black and white ropes that look like spirals are actually concentric circles (circles inside each other).
The Op art (or optical art) style of painting in the mid-1900s used these effects to create the feeling of movement or flashing patterns. Artists like Bridget Riley and Victor Vasarely used these tricks in their work.
Sacred Geometry
Since ancient Greece, some people have believed that God is the "geometer of the world," meaning the universe was created using a geometric plan. This idea comes from the Pythagoreans, who believed everything was arranged by numbers, especially in music.
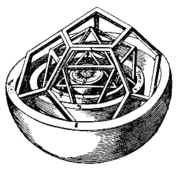
An old drawing from the 1200s shows God drawing the universe with a compass, which might refer to a Bible verse (Proverbs 8:27). In 1596, the astronomer Johannes Kepler even modeled the universe using nested Platonic solids to explain the planets' orbits.
William Blake's Ancient of Days and his painting of Isaac Newton show figures using compasses. These works criticize traditional reason and materialism as being narrow-minded.
Salvador Dalí's 1954 painting Crucifixion (Corpus Hypercubus) shows the cross as a hypercube, representing a divine, four-dimensional perspective. In his The Sacrament of the Last Supper (1955), Christ and his disciples are inside a giant dodecahedron (a 12-sided shape).
-
God the geometer. From the Codex Vindobonensis, around 1220.
-
The creation, with the Pantocrator (God) holding a compass. From the Bible of St Louis, around 1220–1240.
-
Johannes Kepler's Platonic solid model of planetary spacing from Mysterium Cosmographicum, 1596.
-
William Blake's The Ancient of Days, 1794.
See also
In Spanish: Matemáticas y arte para niños
